Hi there.
I’m trying to implement a multivariate Bernoulli distribution that includes correlations between the variables (described in this paper: https://arxiv.org/pdf/1206.1874)
The model looks like this:
@config_enumerate
def discrete_mixture_model(
K,
N,
D_discrete,
X_discrete=None,
):
cluster_proba = numpyro.sample('cluster_proba', dist.Dirichlet(1.0 * jnp.ones(K)))
with numpyro.plate("discrete_cluster", K):
phi = numpyro.sample('phi', dist.Dirichlet(1.0 * jnp.ones(2 ** D_discrete))) #dist.Dirichlet(alpha)) #
with numpyro.plate('data', N):
assignment = numpyro.sample('assignment', dist.CategoricalProbs(cluster_proba))
numpyro.sample(
'obs',
MultivariateBernoulli(phi[assignment, :]),
obs=X_discrete,
)
And the distribution looks like this:
class MultivariateBernoulli(dist.Distribution):
arg_constraints = {'phi': dist.constraints.simplex}
support = dist.constraints.real_vector
def __init__(self, phi):
super(MultivariateBernoulli, self).__init__(batch_shape=phi.shape[:-1], event_shape=phi.shape[-1:])
self.phi = phi
def sample(self, key, sample_shape=()):
raise NotImplementedError
def log_prob(self, value):
return jax.scipy.special.xlogy(
jnp.array(
[jnp.array([v[j] for v, j in zip(zip(value.T, (1-value).T), i)]).prod(axis=0)
for i in itertools.product(*[[0,1] for _ in range(value.shape[-1])])]
).T,
self.phi
).sum(axis=-1)
Essentially the way the distribution works is by having a separate probability for each possible configuration of the variables, hence the presence of the itertools.product in the above. In case this isn’t clear, I’ve implemented the distribution for the specific case of two variables
class MultivariateBernoulli2D(dist.Distribution):
arg_constraints = {'phi': dist.constraints.simplex}
support = dist.constraints.real_vector
def __init__(self, phi):
super(MultivariateBernoulli2D, self).__init__(batch_shape=phi.shape[:-1], event_shape=phi.shape[-1:])
self.phi = phi
def sample(self, key, sample_shape=()):
raise NotImplementedError
def log_prob(self, value):
inds = [slice(None)] * self.phi.ndim
inv_value = 1 - value
return (jax.scipy.special.xlogy(x=inv_value[:, 0] * inv_value[:, 1], y=self.phi[tuple(inds[0:-1] + [0])]) +
jax.scipy.special.xlogy(x=value[:, 0] * inv_value[:, 1], y=self.phi[tuple(inds[0:-1] + [1])]) +
jax.scipy.special.xlogy(x=inv_value[:, 0] * value[:, 1], y=self.phi[tuple(inds[0:-1] + [2])]) +
jax.scipy.special.xlogy(x=value[:, 0] * value[:, 1], y=self.phi[tuple(inds[0:-1] + [3])]))
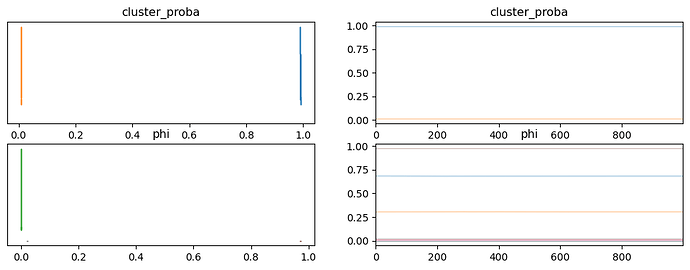
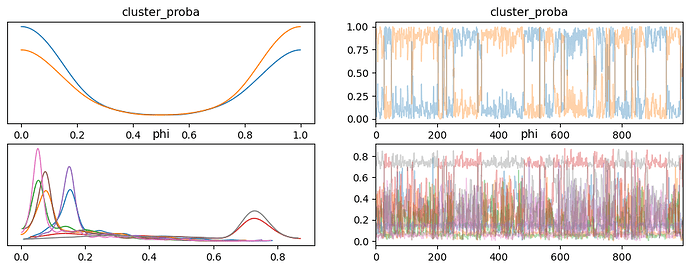
I think I am doing the log_prob calculation correctly as the two methods produce the same values for the same data, but when I try and fit the model using MCMC I don’t get anything like sensible results. The traces of cluster_proba jump back and forth between 0 and 1 during sampling when the clusters are about equally probable. This works with minor modifications (priors from a Beta distribution rather than a Dirichlet distribution for example) when using the builtin Bernoulli distribution that assumes independent variables, and also with a custom distribution that implements the independent Bernoulli distribution.
Does anyone have any ideas about what’s going wrong?
Many thanks!