It’s unclear exactly what you’re looking for, but I can give you some pointers. First, just a note – Pyro is “set up” for pretty much anything you want to do as it’s a universal PPL, you just have to know how to code the model yourself. What I think you mean is that there isn’t necessarily a built-in contrib module for state-space control or something, and I have to agree with you there. That being said, it’s not so hard tot write a state-space control model yourself. I don’t know what kind of state space / HMM you want (discrete-state discrete-likelihood? continuous-state continuous-likelihood? Univariate or multivariate?) so, being biased toward what I tend to use in my own work, here’s a very basic continuous-state continuous-likelihood multivariate state-space control model:
def state_space_control_model(data, N=1, T=2, p=2, u=None):
"""
:param data: (torch.tensor or None) data of shape (T - 1, N, p) or None if prior
:param N: (int) number of observations
:param T: (int) number of timesteps
:param p: (int) dimensionality of data
:param u: (torch.tensor or None) control if observed, or None if control is to be inferred
"""
assert (type(p) is int) and (type(N) is int) and (type(T) is int)
assert (p > 0) and (N > 0) and (T > 0)
# endogenous dynamics
A = pyro.sample(
"A",
dist.Normal(0, 0.1).expand((p, p))
)
# control effect
B = pyro.sample(
"B",
dist.Normal(0, 0.1).expand((p, p))
)
# various noise distributions
eta = pyro.sample(
"eta",
dist.LogNormal(0, 1)
)
state_correlation = pyro.sample(
"state_correlation",
dist.LKJCorrCholesky(p, eta)
)
obs_correlation = pyro.sample(
"obs_correlation",
dist.LKJCorrCholesky(p, eta)
)
state_std = pyro.sample(
"state_std",
dist.LogNormal(0, 1).expand((p,))
)
obs_std = pyro.sample(
"obs_std",
dist.LogNormal(-2, 1).expand((p,))
)
state_cov_tril = torch.mm(torch.diag(state_std), state_correlation)
obs_cov_tril = torch.mm(torch.diag(obs_std), obs_correlation)
if u is None:
controls = torch.empty((T, N, p))
latents = torch.empty((T, N, p))
data_plate = pyro.plate("data_plate", N)
time_markov = pyro.markov(range(1, T))
with data_plate as n:
z_0 = pyro.sample(
"z_0",
dist.MultivariateNormal(torch.zeros(p), scale_tril=state_cov_tril)
)
latents[0] = z_0
if u is None:
u_0 = pyro.sample(
"u_0",
dist.MultivariateNormal(torch.zeros(p), scale_tril=state_cov_tril)
)
controls[0] = u_0
for t in time_markov:
# z[t] = z[t-1] * A + u[t-1] * B + e[t], e[t] ~ MultivariateNormal(...)
# x[t] = z[t] + w[t], w[t] ~ MultivariateNormal(...)
# if controls aren't passed, assume random walk prior for them, so
# u[t] = u[t-1] + b[t], b[t] ~ MultivariateNormal(...)
if u is None:
u_t = pyro.sample(
f"u_{t}",
dist.MultivariateNormal(controls[t - 1], scale_tril=state_cov_tril)
)
this_u = u_t
controls[t] = this_u
else:
this_u = u[t - 1]
z_t = pyro.sample(
"z_t",
dist.MultivariateNormal(
torch.matmul(latents[t - 1], A) + torch.matmul(this_u, B),
scale_tril=state_cov_tril
)
)
latents[t] = z_t
x_t = pyro.sample(
"x_t",
dist.MultivariateNormal(z_t, scale_tril=obs_cov_tril),
obs=data[t - 1] if data is not None else None
)
if u is None:
return latents, controls
return latents
The code is kind of long, but a lot of that is just defining the covariance structure (which pretty much always takes up a lot of real estate). I’m definitely not claiming that this is the state space model you should use or something – for example, I made the rather questionable modeling decision that the covariance structure of the control and of the latent state evolution are identical – but it’s at least something you can start with and modify to fit your needs. Another thing to be aware of with this model is that the coefficient matrices can really go off the rails quickly. If you play with this implementation, you will see that a lot of the time, draws from the prior predictive distribution just diverge after a few timesteps because of overflow. This is because we have not enforced stationarity on the VAR coefficient matrix A or the control matrix B. If you want to know about this, I guess you can read Lutkepohl or something, although do see the Stan docs on maybe why you should not enforce stationarity but rather encourage it. At any rate, here are some draws from the prior predictive, just so you have a sense for what can come out of the model (conditioned on the fact that the sample paths don’t blow up…):
SEED = 2
torch.manual_seed(SEED)
pyro.set_rng_seed(SEED)
latents, controls = state_space_control_model(None, T=100)
...
# plotting code...
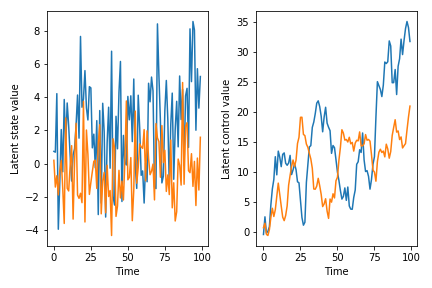
You could fit this model in whatever way comes naturally to you. Since the parameter space will expand pretty quickly, particularly if you want to infer the control policies, you might want to think about using SVI.
Hopefully this helps. Feel free to go on with some more questions and we can work from there.
