Hello everyone,
I’m using numpyro to fit some experimental data to the solution of a differential equation. However, I’ve encountered a problem where, for certain combinations of parameters, the solution is not defined. As you can see from the attached image, these points are marked in orange.
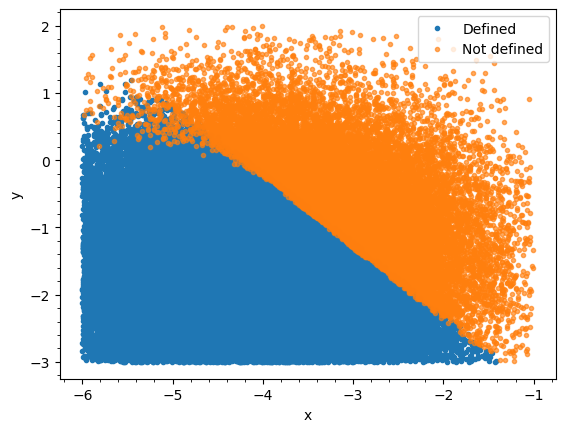
It’s possible to determine in advance with high probability whether the solution will be defined based on the sum of the two variables, i.e. when the sum is less than x the solution will be defined. I want to implement this constraint in my model, code below, but I’m having some difficulty doing so. The only way I have been able to implement this so far is to restrict the parameter range to be within the red bounded region, as below, but this has the disadvantage of ruling out some combinations.
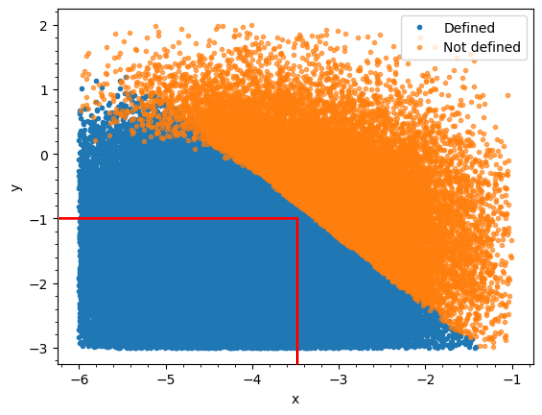
Does anyone know how to constrain the sampling of the parameters, theta[1] and theta[2], in this way, or have any alternative suggestions?
Thank you in advance for any help you can provide
def model(N0, y0, ydata = None):
"""
Bayesian model for the BTDP model.
Parameters
----------
N0: float
Initial value.
y0: float
Offset.
ydata: array
experimental data.
"""
theta = numpyro.sample(
"theta",
Uniform(
low = jnp.array([-8.0, -6.0, -3.0, 0.001]),
high = jnp.array([-4.5, -1.0, 2.0, 0.5])
),
)
#Calculate the TRPL signal and standardise
signal = Differential_eqn(jnp.array([10**theta[0], 0.0, 10**theta[1], 0.0, 0.0, 0.0, 10**theta[2]]), 10**y0, N0)
std_signal = standardise(signal)
#Define the likelihood
numpyro.sample("ydata", dist.Normal(std_signal, jnp.full(shape=(len(std_signal),), fill_value=theta[3])), obs=ydata)