Confused about importance sampling result for a GMM

1

I’ve been starting to learn pyro by applying different inference methods to a Gaussian mixture model (GMM). I am confused about the bad results I’m getting when using importance sampling with a guide fit using SVI to infer the cluster means.

Here are the model and data definitions (taken from tests/infer/mcmc/test_hmc.py):

K = 2

@config_enumerate(default="parallel")
def gmm(data):
    mix_proportions = pyro.sample("phi", dist.Dirichlet(torch.ones(K)))
    with pyro.plate("num_clusters", K):
        cluster_means = pyro.sample("cluster_means",
                                    dist.Normal(torch.arange(float(K)), 1.))
    with pyro.plate("data", data.shape[0]):
        assignments = pyro.sample("assignments", dist.Categorical(mix_proportions))
        pyro.sample("obs", dist.Normal(cluster_means[assignments], 1.), obs=data)
    return cluster_means

# Generate data
N = 100
true_cluster_means = torch.tensor([1., 5.])
true_mix_proportions = torch.tensor([0.4, 0.6])
cluster_assignments = dist.Categorical(true_mix_proportions).sample(torch.Size((N,)))
data = dist.Normal(true_cluster_means[cluster_assignments], 1.0).sample()

I want to infer cluster_means. Next, define the guide and fit with SVI:

def gmm_guide(data):
    weight_param = pyro.param("weight_param", torch.ones(K),
                              constraint=constraints.positive)
    mix_proportions = pyro.sample("phi", dist.Dirichlet(weight_param))
    
    # Fine-tuned initializations
    mean_param = pyro.param("mean_param", torch.tensor([0.9, 3.1]))
    scale_param = pyro.param("scale_param", 0.5*torch.ones(K),
                             constraint=constraints.positive)
    with pyro.plate("num_clusters", K):
        cluster_means = pyro.sample("cluster_means", dist.Normal(mean_param, scale_param))

# Fit guide and create posterior
pyro.clear_param_store()
svi = SVI(model=gmm, guide=gmm_guide,
          optim=optim.Adam({"lr": 0.01, "betas": [0.8, 0.99]}),
          loss=TraceEnum_ELBO(max_plate_nesting=1))

for t in range(3000):
    svi.step(data)

guided_importance_run = Importance(gmm, gmm_guide, num_samples=500).run(data)
guided_posterior = EmpiricalMarginal(guided_importance_run, sites=["cluster_means"])

The SVI loss seems to converge reasonably well.

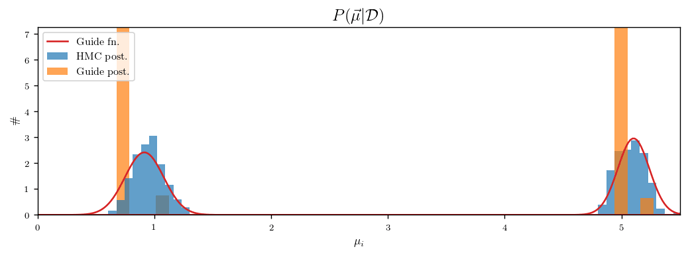
Now I’m drawing 500 samples of cluster_means from guided_posterior and plotting the distributions of the two components. For comparison, I’m also plotting draws from a posterior computed with HMC/MCMC. I’m also visualizing the guide function by plotting two Gaussians with means and standard deviations given by the components of mean_param and scale_param. Here is the result:

posterior_sample_comparison.png1041×388 20.7 KB

I am confused about this plot. All the draws from guided_posterior are the same, even though the guide nearly matches the HMC posterior. The draw is the just highest-probability point from the importance sampling run and is not particularly close to the guide’s mode. Why is this happening?

2

Just a side question: What if you do things this way

svi = SVI(...)
for t in range(3000):
    svi.step(data)

svi.num_samples = 10000
svi_run = svi.run(data)
guided_posterior = EmpiricalMarginal(svi_run, sites=["cluster_means"])
3

That gives very reasonable results! I noticed that SVI.run() fits the guide before collecting traces, so another way to do this is:

svi = SVI(..., num_steps=1000, num_samples=1000)
svi_run = svi.run(data)

In this case the calls to SVI.step() are inside of SVI.run(), so it seems trickier to monitor convergence. Either way, here are the resulting samples from the posterior:

posterior_sample_comparison.png1198×442 23.4 KB

A couple questions/notes:

  • Can you explain why your snippet works, but using the guide with Importance yields the plot in my OP?
  • From the inference tutorial I was under the impression that SVI was mainly used to optimize guide functions. Here it appears it’s being used to perform the importance sampling as well. How should I understand SVI’s role?
  • It seems somewhat confusing that the optimizer can be stepped explicitly by calling SVI.step() as well as implicitly through calls to SVI.run() if num_steps is set.
4

About the plot, I think you can get some reasons when you look at the guided_importance_run.get_normalized_weights() (they are mostly very small). It seems that the likelihood p(data | latent) in your model is too small, which in turn makes unnormalized_weight = p(latent, data) / q(latent) too small. When normalizing, the largest one will dominate the remaining ones.

SVI is used to approximate posterior. Important sampling is used to get an execution of samples with weights, which is in turn used to estimate expectation of some target function w.r.t. “ideal” posterior distribution. So I don’t think that posterior guide (which is learned from SVI or MCMC) is the best guide for important sampling. The best guide depends on the integrand which you need to compute expectation (w.r.t. “ideal” posterior distribution). I think that the tutorial just means that you can use SVI approximated guide as a guide for important sampling (this is good for many cases). If it makes you confused, I suggest to raise an issue to clarify it in the tutorial.

About setting num_steps, I think that it is reasonable. Why do you need to call .step() when you know ahead how many num_steps you need to get the posterior you want? To me, SVI.step is just a convenient function to observe the loss (and to match the pattern of stochastic training). The universal pattern to get posterior in Pyro is: posterior.run(data). It is also totally fine if you run SVI.step for a while, then do .run(data). In that case, you don’t have to touch the default num_steps=0 argument at SVI initialization.

5

Thanks for the response and apologies for the long posts.

I agree with you that the weights seem very small, but my gmm model has the same form as my data generation procedure, so I don’t see an obvious problem. To understand what’s going on, I went through Importance._traces() and computed model_trace.log_prob_sum() myself.

guide_trace = poutine.trace(gmm_guide).get_trace(data)
model_trace = poutine.trace(poutine.replay(gmm, trace=guide_trace)).get_trace(data)

# Trace parameters
cluster_means_tr = guide_trace.nodes["cluster_means"]["value"]

# Prior log probs for weights and means
phi_prior_lp = dist.Dirichlet(torch.ones(K)).log_prob(phi_tr).sum()
cluster_means_prior_lp = dist.Normal(
    5.*torch.arange(float(K)), 1.).log_prob(cluster_means_tr).sum()  # I've changed this since the OP
lps = phi_prior_lp + cluster_means_prior_lp  # total log prob

for d in data:
    p = torch.tensor(0.)
    # Sum probabilities for each cluster
    for c in [0, 1]:
        p += (dist.Categorical(phi_tr).log_prob(torch.tensor(c)).exp() *
              dist.Normal(cluster_means_tr[c], 1.).log_prob(d).exp())
    lps += p.log()

The log probabilities I obtained were significantly larger than those returned by model_trace.log_prob_sum() in that line. Repeating this calculation to gather a list of cluster_means from the guide_traces and the respective hand-computed log probability lps gives a histogram that matches very well with the posterior computed using HMC.

I am confused by the difference in the probabilities. I’ve been looking at the traces’ nodes to try to understand this. It seems like the small probabilities returned by model_trace.log_prob_sum() are related to cluster assignments. For example, for a representative iteration of the above block of code, I find:

guide_trace.nodes["cluster_means"]["value"]
>>> tensor([ 0.0188,  5.2066])
model_trace.nodes["obs"]["value"][0:5]
>>> tensor([-1.4910,  2.0026,  4.1350,  4.7100,  5.0414])
model_trace.nodes["assignments"]["value"][0:5]
>>> tensor([ 1,  0,  0,  0,  0])

Generally it appears that many of the cluster assignments are incorrect. But why does the assignments node exist in the first place? Shouldn’t the @config_enumerate(...) decorator on the model result in pyro marginalizing over these anyways?

6

@config_enumerate(...) does not work with Important sampling. You might create an EnumImportant class as follows:

class EnumImportance(Importance):
    def _traces(self, *args, **kwargs):
        loss = pyro.infer.TraceEnum_ELBO()
        for i in range(self.num_samples):
            model_trace, guide_trace = next(loss._get_traces(self.model, self.guide, *args, **kwargs))
            log_weight = pyro.infer.traceenum_elbo._compute_dice_elbo(model_trace, guide_trace)
            yield (model_trace, log_weight)

And use this class instead of Importance. I’ll not recommend using it though (because it is not an official one).

7

Ok, that explains the issue I was running into! Thanks for the example.

So if I have my heart set on using Importance here, it seems I should just modify the guide to estimate the cluster assignments:

def gmm_guide(data):
    ...
    with pyro.plate('data', len(data)):
        assignment_probs = pyro.param('assignment_probs', torch.ones(len(data), K) / K,
                                      constraint=constraints.unit_interval)
        pyro.sample('assignments', dist.Categorical(assignment_probs))

I’ve checked that the assignment_probs parameter is fit by SVI even if I leave the @config_enumerate in the model definition and use the TraceEnum_ELBO loss function. I’m a bit confused about why this works since I thought @config_enumerate required the sites being enumerated not to appear in the guide. Am I overriding this by including the pyro.sample('assignments', ...) statement?

The GMM example does this as well, but decorates the guide as well as the model with @config_enumerate. Why is the decorator used twice?

8

AFAIK, many things will work if you don’t enable pyro.enable_validation().