Conditional Multivariate Normal

Misc.
1

Hi,
I’m trying to model a multivariate normal distribution and calculate the conditional. While we have closed form expressions (following is copied from Wikipedia article on MVN)

\begin{pmatrix} X_1 \\ X_2 \end{pmatrix} \sim \mathcal{N} \left( \begin{pmatrix} \mu_1 \\ \mu_2 \end{pmatrix} , \begin{pmatrix} \sigma^2_1 & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma^2_2 \end{pmatrix} \right)

We then have:
\operatorname{E}(X_1 \mid X_2=x_2) = \mu_1 + \rho \frac{\sigma_1}{\sigma_2}(x_2 - \mu_2)

\operatorname{var}(X_1 \mid X_2 = x_2) = 1-\rho^2

I am trying to model the same using Pyro conditionals (again for learning purposes only as the closed form is well defined).

import pyro
dist = pyro.distributions


def model():
    loc = torch.tensor([0.0, 0.0])
    cov = torch.tensor([[1.0, 0.5], [0.5, 2]])

    X = pyro.sample(
        "X_MVN",
        dist.MultivariateNormal(loc=loc, covariance_matrix=cov),
    )

I can use rejection sampling and get the conditional, but that’s perhaps too resource intensive?!

from pyro.poutine import trace
with pyro.plate("samples", 100000, dim=-2):
    tr = trace(model).get_trace()
x = tr.nodes['X_MVN']['value'].squeeze()
x_conditional = x[torch.where((1.99 < x[:, 0])&(x[:, 0] < 2.01))]
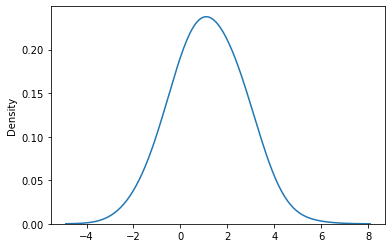
sns.kdeplot(x_conditional[:, 1], bw_adjust=2)

This produces the expected plot.
4

Question

How can I use pyro.condition to obtain P(X2|X1=1)? Or, is there a better solution (ignoring the closed form conditional expression for now)?

For example,

from pyro import condition
cond = condition(model, {"X_MVN": torch.tensor([1., ?])})
cond()

I’d like to replace the ? in the above line to say None, so that I am conditioning on X1 = 2 and then finding the conditional of X2?