Hi all,
I am playing around with the do-operator while following along with the lecture Causality: Jonas Peters, Part 1 and the post by inFERENCe toy example.
models
def model_01():
x = numpyro.sample("x", dist.Normal(0, 1))
_y = numpyro.sample("_y", dist.Normal(0, 1))
y = numpyro.deterministic("y", x + 1 + jnp.sqrt(3) * _y)
return x, y
def model_02():
_y = numpyro.sample("_y", dist.Normal(0, 1))
_x = numpyro.sample("_x", dist.Normal(0, 1))
y = numpyro.deterministic("y", 1 + 2 * _y)
x = numpyro.deterministic("x", (y - 1) / 4 + jnp.sqrt(3) * _x / 2)
return x, y
def model_03():
_z = numpyro.sample("_z", dist.Normal(0, 1))
_y = numpyro.sample("_y", dist.Normal(0, 1))
y = numpyro.deterministic("y", _z + 1 + jnp.sqrt(3) * _y)
x = numpyro.deterministic("x", _z)
return x, y
Given the three models above, I can see that both the joint distribution and the conditional, P(Y | X = 3) are equal.
With this toy example, I wanted to see how numpyro.handlers.do and numpyro.handlers.condition differ expecting the intervention P_{do(X = 3)} \ne P(Y | X = 3). As in the blog post, I can show that P_{do(X = 3)} \ne P(Y | X = 3) is true by comparing the between the Figure 1 and 2, posterior of y. The intervention and conditioning differ because each model have different structural causal equations.
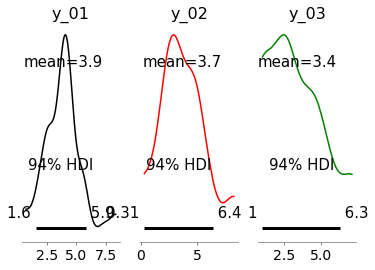
Figure 1: P(Y|X=3) for each model (the distributions look off because of the low number of samples. I am just trying to be consistent with the blog post)
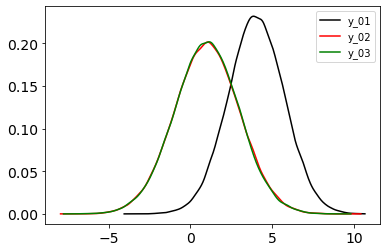
Figure 2: P_{do(X = 3)} for each model.
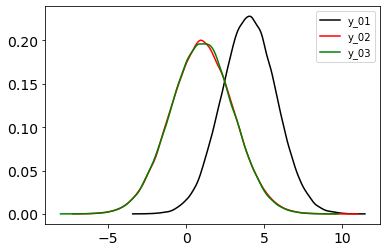
Figure 3: numpyro.handlers.condition(..., data={"x": 3}) for each model.
What surprises me is that numpyro.handlers.do and numpyro.handlers.condition result in the same posterior for y. Is this expected? I don’t think an intervention with a do-operator is the same as Bayesian inference so is this result expected because of the mechanism/implementation of condition and do?
Link to the full notebook.
Note: Maybe this toy problem is not the greatest example because of at least two complications I came across.
- In Jonas Peters lecture and slides he emphasizes that P_{do(X = x)} \ne P(. | X = x), yet in the simplest X → Y model intervention and conditioning do equal… I think this is a simple proof…
- At times I am using
numpyro.handlers.conditionon a deterministic site which I think may cause some issues, see this post.