Dear pyro experts.
I’m inspired by the bayesian CNN example from @neerajprad, and @udion incorrect log_prob dimension · Issue #1409 · pyro-ppl/pyro · GitHub
I made the model deeper by adding more layers,
and tried to infer weights. However, it seems like the training got stuck at some point and the loss doesn’t decrease any more.
When I parameterize only the output layer using “random_module”, it works well. The predictions looked pretty good. However when I parameterize all the weights in the model, it seems like I cannot train them correctly.
Please let me know if you can see anything wrong in this code.
The Regression Model.
import os
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable as V
import pyro
from pyro.distributions import Normal
from pyro.infer import SVI, Trace_ELBO
from pyro.optim import Adam
# for CI testing
smoke_test = ('CI' in os.environ)
pyro.enable_validation(True)
class RegressionModel(nn.Module):
def __init__(self, indim, outdim):
# p = number of features
super(RegressionModel, self).__init__()
self.conv1 = nn.Conv1d(1, 2, kernel_size=3, stride=1, padding=1)
self.conv2 = nn.Conv1d(2, 1, kernel_size=3, stride=1, padding=1)
self.linear1 = nn.Linear(indim, indim)
self.linear2 = nn.Linear(indim, indim)
self.linear3 = nn.Linear(indim, indim)
self.linear4 = nn.Linear(indim, indim)
self.linear5 = nn.Linear(indim, indim)
self.linear6 = nn.Linear(indim, indim)
self.softplus = nn.Softplus()
self.linear = nn.Linear(indim, outdim)
def forward(self, x):
y = self.conv1(x.cuda())
y = self.conv2(y.cuda())
y = self.softplus(self.linear1(y))
y = self.softplus(self.linear2(y))
y = self.softplus(self.linear3(y))
y = self.softplus(self.linear4(y))
y = self.softplus(self.linear5(y))
y = self.softplus(self.linear6(y))
y = self.linear(y.cuda())
# print('fwd:', y.size())
return y.cuda()
regression_model = RegressionModel(10, 5).cuda()
Creating dataset,
N = 500 # size of toy data
indim = 10
outdim = 5
def build_linear_dataset(N, indim, outdim, noise_std=0.01):
X = np.random.rand(N, indim)
# w = 3
w = 3 * np.ones((indim, outdim))
# b = 1
b = 1*np.ones((N, outdim))
y = np.matmul(X, w)
# print(y.shape)
y = y + b + np.random.normal(0, noise_std, size=(N, outdim))
# print(y.shape)
y = y.reshape(N, outdim)
X, y = torch.tensor(X).type(torch.Tensor), torch.tensor(y).type(torch.Tensor)
data = torch.cat((X, y), 1)
return data.cuda()
Model function,
def model(data):
priors = dict()
for n, p in regression_model.named_parameters():
if "linear" in n:
i = 2
elif "conv" in n:
i = 3
if "weight" in n:
priors[n] = pyro.distributions.Normal(
loc = torch.zeros_like(p),
scale = torch.ones_like(p)).independent(i)
elif "bias" in n:
priors[n] = pyro.distributions.Normal(
loc = torch.zeros_like(p),
scale = torch.ones_like(p)).independent(1)
# lift module parameters to random variables sampled from the priors
lifted_module = pyro.random_module("module", regression_model, priors)
# sample a regressor (which also samples w and b)
lifted_reg_model = lifted_module()
with pyro.iarange("map", N):
# with pyro.plate("map", N):
x_data = data[:, :-5].view(N,1,-1)
y_data = data[:, -5:].view(N, 1, -1)
# run the regressor forward conditioned on data
prediction_mean = lifted_reg_model(x_data)
# condition on the observed data
pyro.sample("obs",
Normal(prediction_mean, 0.1*torch.ones(data.size(0), 1, outdim)).independent(2),
obs=y_data)
Guide function,
softplus = torch.nn.Softplus()
def guide(data):
priors = dict()
for n, p in regression_model.named_parameters():
if "linear" in n:
i = 2
elif "conv" in n:
i = 3
if "weight" in n:
loc = pyro.param("mu_" + n, torch.randn_like(p))
scale = torch.abs(pyro.param("sigma_" + n, softplus(torch.randn_like(p))))
priors[n] = pyro.distributions.Normal(loc = loc, scale = scale).independent(i)
elif "bias" in n:
loc = pyro.param("mu_" + n, torch.randn_like(p))
scale = torch.abs(pyro.param("sigma_" + n, softplus(torch.randn_like(p))))
priors[n] = pyro.distributions.Normal(loc = loc, scale = scale).independent(1)
lifted_module = pyro.random_module("module", regression_model, priors)
# sample a regressor (which also samples w and b)
return lifted_module()
optim = Adam({"lr": 0.005})
svi = SVI(model, guide, optim, loss=Trace_ELBO())
Training,
num_iterations = 10000 if not smoke_test else 2
def main():
pyro.clear_param_store()
data = build_linear_dataset(N, 10, 5)
for j in range(num_iterations):
# print(j)
# calculate the loss and take a gradient step
loss = svi.step(data)
if j % 100 == 0:
print("[iteration %04d] loss: %.4f" % (j + 1, loss / float(N)))
if __name__ == '__main__':
main()
Output, (last 1,500 steps)
[iteration 8501] loss: 1946.6154
[iteration 8601] loss: 1997.6739
[iteration 8701] loss: 1949.1104
[iteration 8801] loss: 1946.3191
[iteration 8901] loss: 1957.8130
[iteration 9001] loss: 1947.1460
[iteration 9101] loss: 1947.1499
[iteration 9201] loss: 1946.7201
[iteration 9301] loss: 1946.1788
[iteration 9401] loss: 1946.3404
[iteration 9501] loss: 1958.0493
[iteration 9601] loss: 1946.2720
[iteration 9701] loss: 1955.1269
[iteration 9801] loss: 1946.7895
[iteration 9901] loss: 1946.3990
Evaluation,
num_samples = 100
sampled_models = [guide(None) for _ in range(num_samples)]
X = np.random.rand(200, indim)
w = 3 * np.ones((indim, outdim))
b = 1*np.ones((200, outdim))
y = np.matmul(X, w)
# print(y.shape)
y = y + b
from sklearn.metrics import mean_absolute_error
x_data, y_data = torch.tensor(X).type(torch.Tensor).unsqueeze(1), torch.tensor(y).type(torch.Tensor).unsqueeze(1)
predictions = []
labels = []
MAE = []
for model in sampled_models:
pred = []
true = []
# for batch_id, data_test in enumerate(test_loader):
pred.append(model(x_data).cpu().detach().view(-1,5))
true.append(torch.tensor(y_data).view(-1,5))
mae = mean_absolute_error(torch.cat(true), torch.cat(pred))
predictions.append(torch.cat(pred).numpy())
labels.append(torch.cat(true).numpy())
MAE.append(mae)
%matplotlib inline
import seaborn as sns
import numpy as np
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
# import seaborn as sns
from collections import defaultdict
from matplotlib import pyplot as plt
from IPython.display import clear_output
targets_pred = predictions[0].flatten() #torch.cat(pred).view(-1)
targets_val = labels[0].flatten() #torch.cat(true).view(-1)
mae = mean_absolute_error(targets_val, targets_pred)
rmse = np.sqrt(mean_squared_error(targets_val, targets_pred))
r2 = r2_score(targets_val, targets_pred)
# Report
print('MAE = %.2f eV' % mae)
print('RMSE = %.2f eV' % rmse)
print('R^2 = %.2f' % r2)
# Plot
lims = [0, 30]
grid = sns.jointplot(targets_val.reshape(-1), targets_pred,
kind='hex',
bins='log',
extent=lims+lims)
_ = grid.ax_joint.set_xlim(lims)
_ = grid.ax_joint.set_ylim(lims)
_ = grid.ax_joint.plot(lims, lims, '--')
# _ = grid.ax_joint.set_xlabel('DFT $\Delta$E [eV]')
# _ = grid.ax_joint.set_ylabel('CGCNN $\Delta$E [eV]')
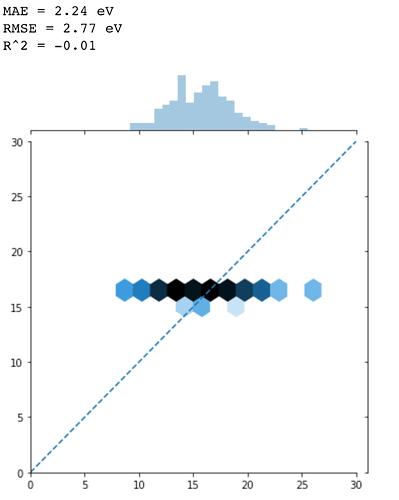
It looks like It cannot predict anything but predicts every data point as ~16
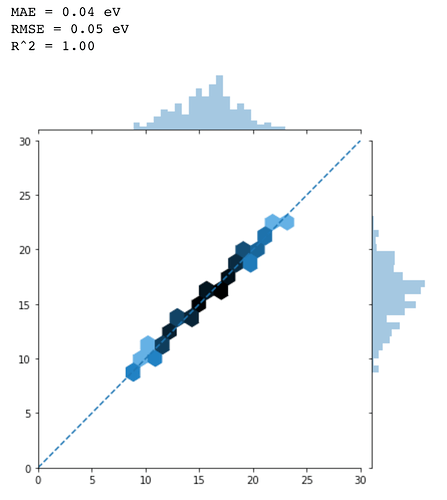
When I parameterize only the output layer (self.linear in this model),
The results looks very good.