Best practice for variational inference of covariance matrices

Misc.
1

I would like to infer covariance matrices using variational inference while maintaining control over the variational family (i.e. not using auto guides). As (inverse) Wishart distributions aren’t yet available, I’ve been using a scale/correlation decomposition in the model like so (the gamma prior of course needs replacing with something more flexible).

# p is the number of dimensions of the covariance matrix.

def model():
    # Sample the scales of the covariance matrix.
    d = dist.Gamma(1, 1).expand([p]).independent(1)
    scale = pyro.sample('scale', d)

    # Sample the correlation matrix.
    d = dist.LKJCholesky(p, 1)
    cholesky_corr = pyro.sample('cholesky_corr', d)

    # Evaluate the Cholesky decomposition of the covariance matrix.
    cholesky_cov = cholesky_corr * torch.sqrt(scale[:, None])

    # Rest of model goes here...

In the guide, I’ve used a transformed distribution for the correlation matrix like so.

def guide():
    # Parametrise the variational distribution for the scales.
    concentration = pyro.param('scale_concentration', 10 * torch.ones(p), 
                               constraint=dist.constraints.positive)
    rate = pyro.param('scale_rate', 10 * torch.ones(p), 
                      constraint=dist.constraints.positive)
    d = dist.Gamma(concentration, rate).independent(1)
    scale = pyro.sample('scale', d)

    # Parametrise the variational distribution for the covariance.
    q = p * (p - 1) // 2  # Number of parameters needed to parametrise a correlation matrix.
    loc = pyro.param('cholesky_corr_loc', torch.zeros(q))
    cov = pyro.param('cholesky_corr_cov', 1e-2 * torch.eye(q), 
                     constraint=dist.constraints.positive_definite)
    d = dist.MultivariateNormal(loc, cov)
    d = dist.TransformedDistribution(d, dist.transforms.CorrCholeskyTransform())
    cholesky_corr = pyro.sample('cholesky_corr', d)
    
    # Rest of guide goes here...

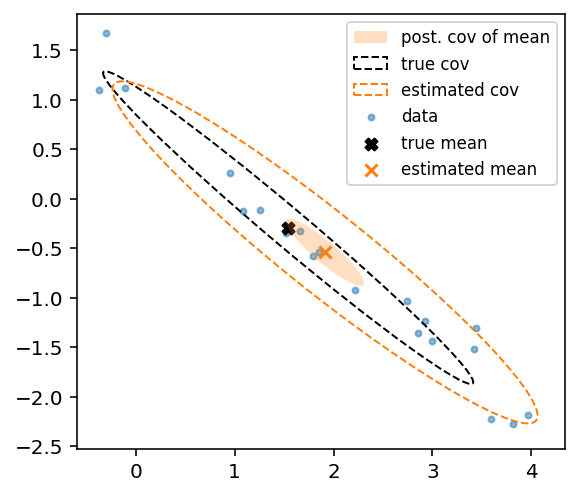
This seems to work fine as I can infer the covariance of a multivariate Gaussian (see below), but are there better/easier approaches than the above?

image

1 Like
2

I like your approach. We don’t know about the posterior of covariance matrix so we use SVI and approximate the base distribution d = CorrCholeskyTransform.inv(posterior_of_correlation_matrix). You are flexible to choose a variational distribution for d (in your case, you choose MVN). You can make that variational distribution more complicated if you want but I feel that MVN (or just simply diagonal normal) is already good.

Even if Wishart distribution is available, we need to use an assumption that the posterior can be approximated by a Wishart distribution. I just feel that it is a strong (but maybe convenient) assumption.

1 Like