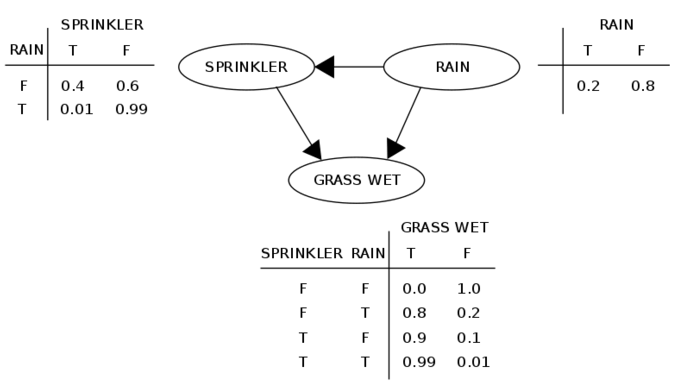
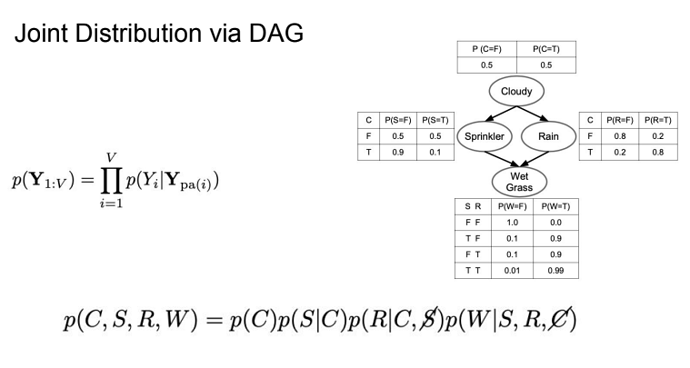
I have been teaching a machine learning course and part of it is statistical rethinking in pyro. While following the book students struggled as a beginner even in 2nd chapter.
I went through multiple posts here and else where so that I can teach them some aspects of directed graphical model and pyro basics. Maybe I will record the video and share sometime in future.
So I wanted to share my learnings and the consolidated beginner tutorial for teaching DGM (Directed Graphical Model) with discrete variables and CPTs (Conditional Probability Tables). You can find my slides here ( M7-S1a DGM Discrete case, Sampling from Joint + Conditional, Inference, Code Walkthrough.pdf - Google Drive )
Please give feedback or let me know if there are any mistakes. This is just a consolidation of various post in pyro forum.
Tutorials for Discrete Directed Graphical Model.
Model Specification
import math
import torch
import pyro
import pyro.distributions as dist
def model(rain=None, sprinkler=None, grasswet=None):
s_rain = pyro.sample('raining', dist.Bernoulli(0.2), obs=rain)
sprinkler_probs = ( 0.01 * s_rain) + (0.4 * (1 - s_rain))
s_sprinkler = pyro.sample('sprinkler', dist.Bernoulli(sprinkler_probs), obs=sprinkler)
grasswet_probs = 0. * (1 - s_sprinkler) * (1 - s_rain) + 0.8 * (1 - s_sprinkler) * s_rain \
+ 0.9 * s_sprinkler * (1 - s_rain) + 0.99 * s_sprinkler * s_rain
s_grasswet = pyro.sample('grasswet', dist.Bernoulli(grasswet_probs), obs=grasswet)
return s_rain, s_sprinkler, s_grasswet
F, T = torch.tensor(0.), torch.tensor(1.)
pyro.render_model(model, model_args=(F,F,F,), render_params=True, render_distributions=True)
# this is used when we have discrete random variable with are latent or needs marginalization
enum_model = pyro.infer.config_enumerate(model)
guide = lambda **kwargs: None
elbo = pyro.infer.TraceEnum_ELBO(max_plate_nesting=0)
Test CPTs from the above diagram (results directly readable from CPTs)
conditional_marginals = elbo.compute_marginals(enum_model, guide)
print(conditional_marginals)
print("p(rain=T):", conditional_marginals["rain"].log_prob(T).exp())
OrderedDict([(‘rain’, Bernoulli(logits: -1.3862944841384888)), (‘sprinkler’, Bernoulli(logits: -0.7445956468582153)), (‘grasswet’, Bernoulli(logits: -0.20721828937530518))])
p(rain=T): tensor(0.2000)
conditional_marginals = elbo.compute_marginals(enum_model, guide, rain=T)
print("p(sprinkler=T|rain=T):", conditional_marginals["sprinkler"].log_prob(T).exp())
p(sprinkler=T|rain=T): tensor(0.0100)
conditional_marginals = elbo.compute_marginals(enum_model, guide, sprinkler=T, rain=T)
print("p(grasswet=T|sprinkler=T,rain=T):", conditional_marginals["grasswet"].log_prob(T).exp())
p(grasswet=T|sprinkler=T,rain=T): tensor(0.9900)
Compute conditional marginals
conditional_marginals = elbo.compute_marginals(enum_model, guide, sprinkler=F, grasswet=F)
p_r_T_given_s_F_g_F = conditional_marginals["rain"].log_prob(T).exp()
print("p(rain=T|sprinkler=F,grasswet=F):", p_r_T_given_s_F_g_F)
print("p(rain=F|sprinkler=F,grasswet=F):", 1 - p_r_T_given_s_F_g_F)
p(rain=T|sprinkler=F,grasswet=F): tensor(0.0762)
p(rain=F|sprinkler=F,grasswet=F): tensor(0.9238)
conditional_marginals = elbo.compute_marginals(enum_model, guide, rain=T)
print("p(sprinkler=T|rain=T):", conditional_marginals["sprinkler"].log_prob(T).exp())
print("p(grasswet=T|rain=T):", conditional_marginals["grasswet"].log_prob(T).exp())
p(sprinkler=T|rain=T): tensor(0.0100)
p(grasswet=T|rain=T): tensor(0.8019)
Since compute_marginal(.) cannot have joint conditional distribution (e.g. P(grasswet=F,sprinkler=F | rain=T ) or p(grasswet=F,sprinkler=F) ), so we compute joint distribution and marginals separately and use bayes rule to get desired probabilities.
Use Bayes Theorem
P(rain=F, sprinkler=F, wetgrass=F) = P(rain=F) P(sprinkler=F|rain=F) P(wetgrass=F|sprinker=F,rain=F)
This formula can be use to verify that joint distribution calculation is correct. (0.80.61.0=0.48)
# compute p(rain=F,grasswet=F,sprinkler=F)
# from CPT 0.8*0.6*1.0 = P(rain=F)*P(sprinkler=F|rain=F)*P(wetgrass=F|sprinker=F,rain=F)
p_rain_F_sprinkler_F_grasswet_F = pyro.poutine.trace(model).get_trace(F, F, F).log_prob_sum().exp()
print("p(rain=F,sprinkler=F,grasswet=F):", p_rain_F_sprinkler_F_grasswet_F)
p(rain=F,sprinkler=F,grasswet=F): tensor(0.4800)
# compute p(grasswet=F,sprinkler=F)
p_sprinkler_F_grasswet_F = math.exp(-elbo.loss(enum_model, guide, sprinkler=F, grasswet=F))
Using bayes rule we get, p(rain=F|sprinkler=F,grasswet=F)
# compute p(rain=F|sprinkler=F,grasswet=F)
print("p(rain=F|sprinkler=F,grasswet=F):", p_rain_F_sprinkler_F_grasswet_F / p_sprinkler_F_grasswet_F)
p(rain=F|sprinkler=F,grasswet=F): tensor(0.9238)
As an exercise do the same thing for
