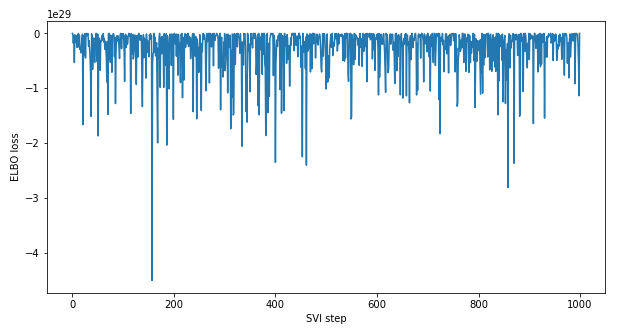
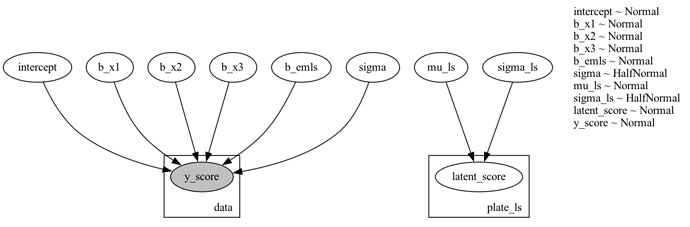
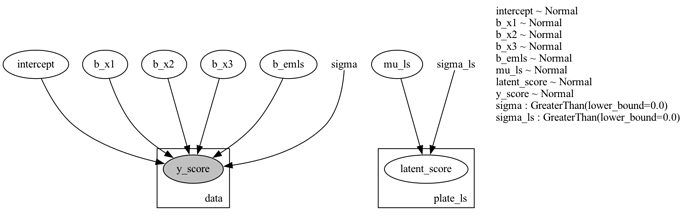
The linear regression model below is currently not converging based on ELBO Loss. I’m using simulated data to test the model, and I’m not sure if the model is appropriately setup.
About the input data - each row in the data corresponds to one person, and the columns are attributes (i.e. x1, x2, x3, and y). Also, I’m attempting to use an associated network dataset (edges_df) to infer a latent impact score of the an individual’s connections, taking the mean impact score of a given individual’s connections as an input to the regression model.
About the outputs - in addition to estimating the regression coefficients, I would like to estimate the latent impact scores for each person. I’m looking for advice to improve the current model or an alternative approach that would yield valid and reliable results.
def model(person_idx, edges_df, x1, x2, x3, y=None):
"""
person_idx: person index (i.e. unique identifier for each person)
edges_df: Pandas dataframe with "source" and "target" columns. The values in
the "target" column are lists of edges, e.g. [2, 17, 39]. Edge values
are based on person_idx.
x1 - x3: numeric input variables
y: numeric target
"""
# Coefficients
intercept = pyro.sample("intercept", dist.Normal(0., 1.0))
b_x1 = pyro.sample("b_x1", dist.Normal(0., 1.0))
b_x2 = pyro.sample("b_x2", dist.Normal(0., 1.0))
b_x3 = pyro.sample("b_x3", dist.Normal(0., 1.0))
b_emls = pyro.sample("b_emls", dist.Normal(0., 1.0))
sigma = pyro.sample("sigma", dist.HalfNormal(1.0))
# A unique latent score for each person
mu_ls = pyro.sample("mu_ls", dist.Normal(0.0, 1.0))
sigma_ls = pyro.sample("sigma_ls", dist.HalfNormal(1.0))
n_people = len(person_idx)
with pyro.plate("plate_ls", n_people):
latent_score = pyro.sample("latent_score", dist.Normal(mu_ls, sigma_ls))
# Mean latent score of edges
edges_mean_latent_impact_score = torch.empty_like(x1)
for p in person_idx:
# Returns list of edges for person p
p_edges = edges_df.loc[edges_df['source'] == p, 'target']
num_p_edges = len(p_edges)
if num_p_edges > 0:
p_edges_mean_latent_score = sum([latent_score[e] for e in p_edges]) / num_p_edges
edges_mean_latent_impact_score[p] = p_edges_mean_latent_score
else:
# Set value to 0 (i.e. neutral score) for those with no edges
edges_mean_latent_impact_score[p] = 0
mean = \
intercept +\
b_x1 * x1 +\
b_x2 * x2 +\
b_x3 * x3 +\
b_emls * edges_mean_latent_impact_score
with pyro.plate("data", len(x1)):
return pyro.sample("y_score", dist.Normal(mean, sigma), obs=y)
Plate Model PNG:
Model Guide and SVI setup:
mvn_guide = pyro.infer.autoguide.AutoMultivariateNormal(model)
svi = pyro.infer.SVI(
model,
mvn_guide,
pyro.optim.Adam({"lr": 0.02}),
pyro.infer.Trace_ELBO())
losses = []
for step in tqdm(range(1000)):
loss = svi.step(person_idx, edges_df, x1, x2, x3, y)
losses.append(loss)
if step % 100 == 0:
logging.info("Elbo loss: {}".format(loss))
# Visualize ELBO loss
plt.figure(figsize=(10, 5))
plt.plot(losses)
plt.xlabel("SVI step")
plt.ylabel("ELBO loss")
ELBO Loss Plot: