Hi, here I have a collection called xs, which contains four candidates matrixes x0, x1 ,x2 and x3 . I also have a target matrix called ydata. The goal is to find which matrix among [x0,x1,x2,x3] is the most similar to the matrix ydata. The strategy is to create a discrete index variable called assignment so that xs[assignment] is the the most similar to ydata.
ydata = torch.tensor([[1.0,2.0,3.0],[6.0,10.0,15.0]])
x0 = torch.tensor([[1.0,2.1,3.0],[6.2,10.0,15.0]])
x1 = torch.tensor([[1.1,2.0,3.0],[6.2,10.0,15.0]])
x2 = torch.tensor([[19.0,29.0,3.0],[69.0,17.0,15.0]])
x3 = torch.tensor([[11.0,25.0,3.0],[7.0,-10.0,15.0]])
xs = torch.stack([x0,x1,x2,x3],dim=-1)
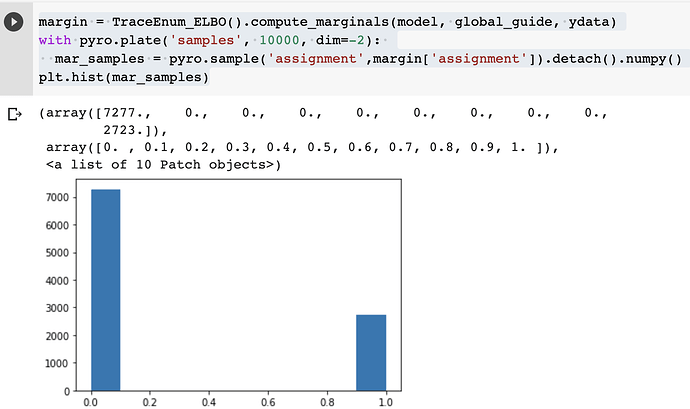
From the actual value we can see that matrixes x0 and x1 are both quite similar to ydata, so I would expect that the distribution of the discrete variable called assignment is approximately 50% on 0 and 50% on 1.
I used the function TraceEnum_ELBO().compute_marginals to get the marginalised discrete distribution of the variable assignment. However, I find a weird thing, which is: if I implement TraceEnum_ELBO().compute_marginals for several times, I can get quite different distributions each time, like:
and
Please note I have fixed the seed and the starting point of SVI. I only trained the SVI once, but runs the TraceEnum_ELBO().compute_marginals several times and obtained different results each time.
I understand that the distribution is obtained by sampling, so I shouldn’t expect that the result is completely the same after each sampling. But I think the problem is from TraceEnum_ELBO().compute_marginals rather than the pyro.sample('assignment',margin['assignment']). step because if I just implement TraceEnum_ELBO().compute_marginals only once and then implement pyro.sample('assignment',margin['assignment']). several times then the distribution is much more stable. I want to understand why TraceEnum_ELBO().compute_marginals gives unstable result.
Below are my code for your reference.
ydata = torch.tensor([[1.0,2.0,3.0],[6.0,10.0,15.0]])
x0 = torch.tensor([[1.0,2.1,3.0],[6.2,10.0,15.0]])
x1 = torch.tensor([[1.1,2.0,3.0],[6.2,10.0,15.0]])
x2 = torch.tensor([[19.0,29.0,3.0],[69.0,17.0,15.0]])
x3 = torch.tensor([[11.0,25.0,3.0],[7.0,-10.0,15.0]])
xs = torch.stack([x0,x1,x2,x3],dim=-1)
locs = xs
# Fixed number of components.
K = 4
@config_enumerate
def model(data):
# Global variables.
weights = pyro.sample('weights', dist.Dirichlet(torch.ones(K)/K))
scale = pyro.sample('scale', dist.LogNormal(0., 2.))
assignment = pyro.sample('assignment', dist.Categorical(weights))
for i in pyro.markov(range(ydata.shape[0])):#pyro.markov(range(len(data))):
for j in pyro.markov(range(ydata.shape[1])):
pyro.sample('obs'+str(i)+'_'+str(j), dist.Normal(locs[:,:,assignment][i,j], scale), obs=ydata[i,j])
After implementing the following training process, the TraceEnum_ELBO converges.
def init_loc_fn(site):
if site["name"] == "weights":
# Initialize weights to uniform.
return torch.ones(K) / K
if site["name"] == "scale":
return torch.tensor([0.5])
if site["name"] == "assignment":
return torch.tensor([0])
raise ValueError(site["name"])
optim = pyro.optim.Adam({'lr': 0.01})
def initialize(seed):
global global_guide, svi
pyro.set_rng_seed(seed)
pyro.clear_param_store()
global_guide = AutoNormal(poutine.block(model, hide=['assignment']),init_loc_fn=init_loc_fn)
svi = SVI(model, global_guide, optim, loss= TraceEnum_ELBO())
return svi.loss(model, global_guide, ydata)
# Choose the best among 100 random initializations.
loss, seed = min((initialize(seed), seed) for seed in range(10))
initialize(seed)
losses = []
for i in range(501 if not smoke_test else 2):
loss = svi.step(ydata)
losses.append(loss)
if i % 10 == 0:
print("ELBO at iter i = "+str(i),loss)
Then I tried to get the marginalised distribution for assignment by
margin = TraceEnum_ELBO().compute_marginals(model, global_guide, ydata)
with pyro.plate('samples', 10000, dim=-2):
mar_samples = pyro.sample('assignment',margin['assignment']).detach().numpy()
plt.hist(mar_samples)
Thank you so much!