The convergence problem of higher-order structure model with latent discrete variable

[qpchen]

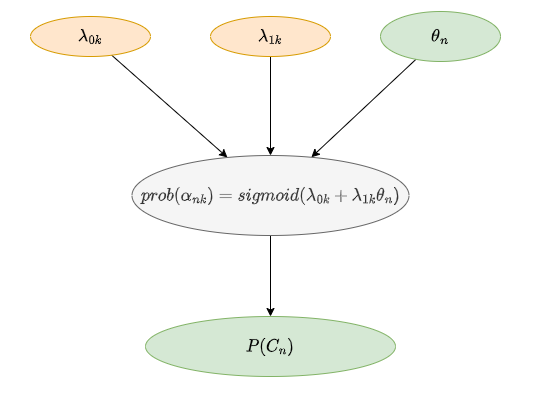
This model is related to the test. Assume there are 2 skills for everyone, and the skill master probability depends on ability \theta_n .

prob(\alpha_{nk}) =sigmod(\lambda_{0k}+\lambda_{1k}\theta_n)

\alpha_{nk} represents whether the nth person has mastered the kth skill, \theta_n is the person’s ability, and \lambda_{0k} and \lambda_{1k} represent the intercept and slope, respectively. The probability of \alpha_{nk} being 1 is as above.

All possible skill patterns can be represented as C row K col matrix, the row is skill pattern category, and the column is skill.

P=\begin{bmatrix} 0 & 0 \\1 & 0 \\0 & 1 \\ 1 & 1 \end{bmatrix}

We can get skill pattern categories by

P(C_n=c) = \sum_1^C \sum_1^KP_{ck}prob(\alpha_{nk}) +[1-P_{ck}][1-prob(\alpha_{nk})]

In my model , see skill pattern category as latent discrete variable and enumeration it. Here is my code:

N,K = 1000,4
all_p = np.array(list(itertools.product(*[[0,1] for i in range(K)])))
def M():
    person_plate = numpyro.plate("person", N, dim=-2)
    skill_plate = numpyro.plate("skill", K, dim=-1)


    with skill_plate:
        # intercept
        lam0 = numpyro.sample("lam_0",dist.Normal(0, 1))
        # slope
        lam1 = numpyro.sample("lam_1",dist.HalfNormal(10))
        

    with person_plate:
        # ability
        theta =  numpyro.sample("theta", dist.Normal(0,1))
        # prob(alpha_{nk})
        alpha_prob = nn.sigmoid(lam0 + theta*lam1)
        # transform prob(alpha_{nk}) to category_prob_{n}
        category_prob = jnp.exp((jnp.log(alpha_prob).dot(all_p.T))+(jnp.log(1-alpha_prob).dot(1-all_p.T)))
        category_prob = category_prob.reshape(N,1,-1)
        # enumerate latent discrete variable
        student_c = numpyro.sample("cat", dist.Categorical(category_prob),infer={"enumerate": "parallel"})

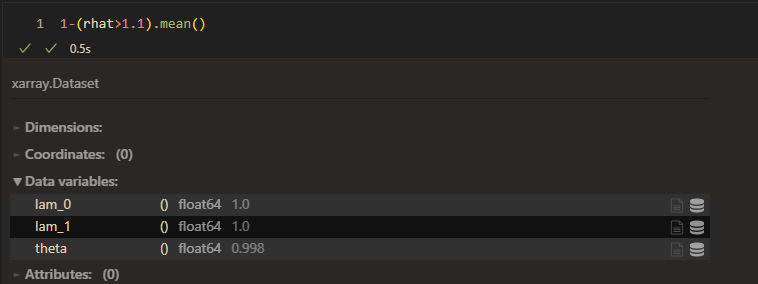
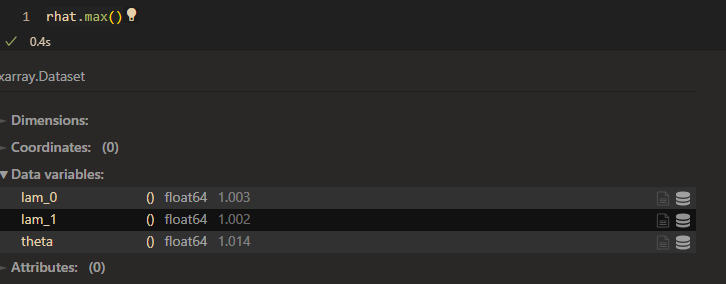
The divergence rate is high and the ess is small when I set prior of \lambda_{1k} as HalfN(0,10).

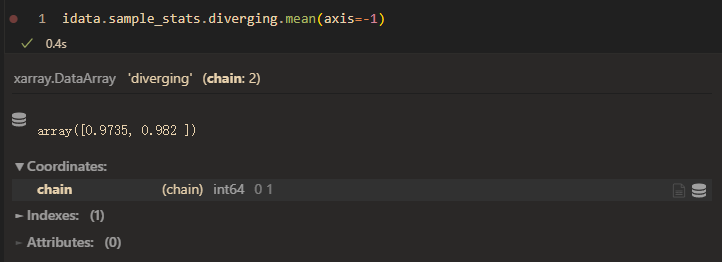
divergence mean:

ess mean:

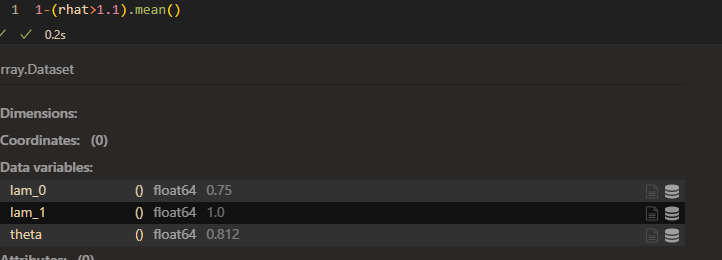
raht:

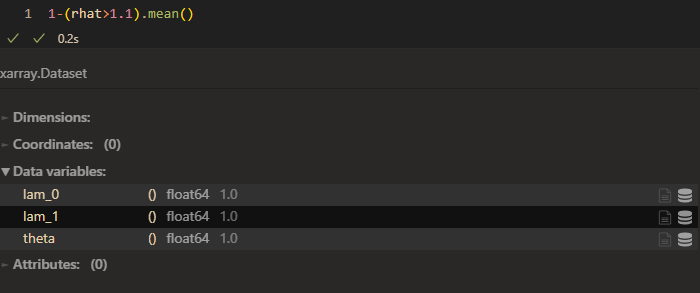
However, the model seems to work good when I set prior of \lambda_{1k} as HalfN(0,1).(small variance)

 lam1 = numpyro.sample("lam_1",dist.HalfNormal(1))

divergence mean:

ess mean:

raht:

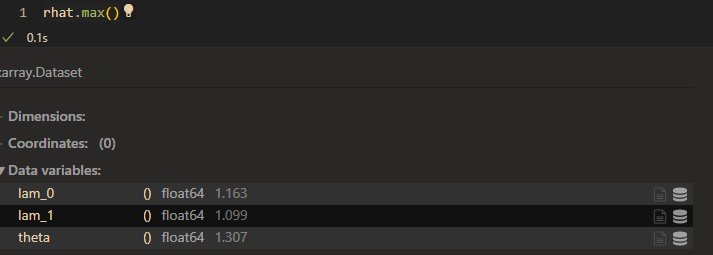
When taking more skill into consideration, the convergence is woser.
skill K = 4

N,K = 1000,4
lam1 = numpyro.sample("lam_1",dist.HalfNormal(10))

divergence mean:

ess mean:

raht:

So my question is：

1. Why small variance prior work but a large variance not work?
2. How can I fix it if I still want to set large variance distribution as prior for the model?

Any help would be greatly appreciated!

[martinjankowiak]

it’s hard to say what’s going on but you might try using 64-bit precision (numpyro.enable_x64()) and use logits to categorize your likelihood instead of probs. you might also consider using some of the tricks described in this tutorial

[qpchen]

Thanks for the quick reply!
After setting the prior to lam1 = numpyro.sample("lam_1",dist.TruncatedNormal(3,10, low=0,high=10)), (numpyro.enable_x64()) and the use of logits instead of prob mitigate the problem of model non-convergence, but do not completely solve it. Setting dense_mass, as well as max_tree_depth, seems to have no effect on convergence.
When numpyro.sample(“cat”, … , obs=xx) is observed, there is no need to marginalize latent discrete variables and the model converges well, so I guess this is likely a problem caused by marginalizing latent discrete variables.

[martinjankowiak]

it may be that discrete enumeration makes the problem very multimodal. hard to say. you might also try numpyro.infer.DiscreteHMCGibbs and numpyro.infer.MixedHMC
although these might struggle as well, especially if you have lots of discrete variables

[qpchen]

I also tried both samplers, however numpyro.infer.DiscreteHMCGibbs and numpyro.infer.MixedHMC were very slow, which is why I transferred to the NUTS algorithm for parameter estimation of this model.

I have found references for numpyro.infer.MixedHMC, are there any references or other information about numpyro.infer.DiscreteHMCGibbs, I would like to know more about numpyro.infer.DiscreteHMCGibbs.

Thanks in advance!

[fehiepsi]

I’m not sure why you need to use NUTS and marginalize cat here. If you want to draw samples from your model M, you can use Predictive.

[qpchen]

Just to simplify the description of the model, actually, each category has a different external representation and therefore needs to be marginalized in cat.

[fehiepsi]

If cat is the latent variable, to marginalize cat, you can remove that variable from the model, then use Predictive to sample the parameters from priors. If cat is an observed variable, you need to provide the values inside the model and use MCMC to sample the other latent variables, so no need to enumerate here. It seems to me that you can just simply use Predictive to sample from priors.

[qpchen]

Thanks for your patience. I still need help with the worse convergence of this model. Observed variables are associated with cat, so I am not sure if I can remove cat from my model and how to do this.
This is a more detailed model code.

import argparse
import os

import numpy as np
import jax
from jax import nn, random, vmap
import jax.numpy as jnp
import pandas as pd
import numpyro
from numpyro import handlers
import numpyro.distributions as dist
from numpyro.infer import MCMC, NUTS, Predictive, DiscreteHMCGibbs, MixedHMC, HMC
from numpyro.infer.reparam import LocScaleReparam
from numpyro.ops.indexing import Vindex
from numpyro.handlers import reparam
import itertools
import arviz as az
numpyro.set_host_device_count(32)
import pickle
import sys

N,K = 5000,4
# all possible category for student
all_p = np.array(list(itertools.product(*[[0,1] for i in range(K)])))

#########################################################################################
# correct probability for every(16) category
all_p_correct_prob = np.array([0.37, 0.74, 0.4 , 0.07, 0.09, 0.  , 
                               0.87, 0.93, 0.65, 0.7 , 0.69, 0.96, 
                               0.06, 0.72, 0.36, 0.3 ])
# student category
student_cat = np.random.randint(0, len(all_p), N)
# correct probability for every student
obs_correct_prob = all_p_correct_prob[student_cat]
# observed response
obs_correct = np.random.binomial(1,obs_correct_prob)
############################################################################################

# with numpyro.handlers.seed(rng_seed=0):
def M():
    person_plate = numpyro.plate("person", N, dim=-2)
    skill_plate = numpyro.plate("skill", K, dim=-1)


    with skill_plate:
        # intercept
        lam0 = numpyro.sample("lam_0",dist.Normal(0, 1))
        # slope
        lam1 = numpyro.sample("lam_1",dist.HalfNormal(10))
        

    with person_plate:
        # ability
        theta =  numpyro.sample("theta", dist.Normal(0,1))
        # prob(alpha_{nk})
        alpha_prob = nn.sigmoid(lam0 + theta*lam1)
        # transform prob(alpha_{nk}) to category_prob_{n}
        category_prob = jnp.exp((jnp.log(alpha_prob).dot(all_p.T))+(jnp.log(1-alpha_prob).dot(1-all_p.T)))
        category_prob = category_prob.reshape(N,1,-1)
        # enumerate latent discrete variable
        student_c = numpyro.sample("cat", dist.Categorical(category_prob),infer={"enumerate": "parallel"})
        print(student_c.shape)
        ######################################################################################
        # obs correct probability for every student
        with numpyro.plate("item", 1, dim=-1):

            obs_correct_p = Vindex(jnp.array(obs_correct_prob))[student_c]
            print(obs_correct_p.shape)
            o = numpyro.sample("correct", dist.Bernoulli(obs_correct_p), obs=jnp.array(obs_correct).reshape(-1,1))
        ######################################################################################

        
kernel = NUTS(M)
mcmc = MCMC(kernel, num_warmup=8000, num_samples=2000,num_chains=2)
mcmc.run(random.PRNGKey(0))
with numpyro.handlers.seed(rng_seed=0):
    idata = az.from_numpyro(
                        mcmc,
                        # posterior_predictive=pred
                        )

Content between line #### is something new, the correct probability depends on the category of student.
Convergence result are as follow:
Rhat

diverging

So, Is there a correct way to enumerate latent discrete variables and how can I improve model convergence?
Thanks for your help in advance!