Struggling with using SVI instead of MCMC

numpyro
1

I’ve been at this for several days now.
I have my model defined as following:

def quadratic_model(x: List[float],
                    y: Optional[List[float]] = None,
                    weight: Union[List[float], float] = 1.0,
                    exercise_id: Optional[List[int]] = None,
                    session_id: Optional[List[int]] = None,
                    **kwargs) -> NoReturn:

    exercise_check = exercise_id is not None
    session_check = session_id is not None

    # Global Parameters
    global_intercept = numpyro.sample('global_intercept', dist.Normal(0.0, 1.0))
    global_slope = numpyro.sample('global_slope', dist.Gamma(2.0, 1.0))
    global_curvature = numpyro.sample('global_curvature', dist.HalfNormal(1.0))

    # Exercise Parameters
    if exercise_check:
        global_intercept_scale = numpyro.sample('global_intercept_scale', dist.HalfNormal(1.0))
        global_slope_rate = numpyro.sample('global_slope_rate', dist.HalfNormal(1.0))

        with numpyro.plate('exercise', len(np.unique(exercise_id)), dim = -1):
            exercise_intercept = numpyro.sample('exercise_intercept', dist.Normal(global_intercept, global_intercept_scale))
            exercise_slope = numpyro.sample('exercise_slope', dist.Gamma(global_slope*global_slope_rate, global_slope_rate))
            exercise_curvature = numpyro.sample('exercise_curvature', dist.HalfNormal(1.0/global_curvature))
            
            # Session Parameters
            if session_check:
                exercise_intercept_scale = numpyro.sample('exercise_intercept_scale', dist.HalfNormal(1.0))
                exercise_slope_rate = numpyro.sample('exercise_slope_rate', dist.HalfNormal(1.0))

                with numpyro.plate('session', len(np.unique(session_id)), dim = -2):
                    session_intercept = numpyro.sample('session_intercept', dist.Normal(exercise_intercept, exercise_intercept_scale))
                    session_slope = numpyro.sample('session_slope', dist.Gamma(exercise_slope*exercise_slope_rate, exercise_slope_rate))
                    session_curvature = numpyro.sample('session_curvature', dist.HalfNormal(1.0/exercise_curvature))

    # Parameter Assignments
    intercept = global_intercept
    slope = global_slope
    curvature = global_curvature

    if exercise_check:
        intercept = exercise_intercept[exercise_id]
        slope = exercise_slope[exercise_id]
        curvature = exercise_curvature[exercise_id]

    if (exercise_check) & (session_check):
        intercept = session_intercept[session_id, exercise_id]
        slope = session_slope[session_id, exercise_id]
        curvature = session_curvature[session_id, exercise_id]

    loc = intercept - slope*x - curvature*x**2
    scale = numpyro.sample('error', dist.HalfNormal(1.0))

    with numpyro.plate('observation', len(x)), handlers.scale(scale = weight):
        numpyro.sample('y_est', dist.Normal(loc, scale), obs = y)

Using MCMC I get the following and it looks exactly like I expected:

image
image722×604 53.1 KB

However, when I try to use SVI with the following code, it gets nowhere near the result of MCMC:

quadratic_guide = autoguide.AutoNormal(quadratic_model, init_loc_fn = autoguide.init_to_median, init_scale = 0.01)

svi = infer.SVI(model = quadratic_model,
                guide = quadratic_guide,
                optim = optim.Adam(step_size = 0.01),
                loss = infer.Trace_ELBO())

num_samples = 1000
svi_result = svi.run(rng_keys[2], num_samples, **data)

svi_posterior_predictive_fn = infer.Predictive(model = quadratic_model,
                                               guide = quadratic_guide,
                                               num_samples = num_samples,
                                               batch_ndims = 2)
svi_posterior_predictive = svi_posterior_predictive_fn(rng_keys[5], **data)

predictions = svi_posterior_predictive_fn(rng_keys[5], **pred_dict)

image
image722×604 64.7 KB

I’ve tried all available autoguides; step_size & init_scale from 0.0001 to 1.0; with no major difference.

1 Like
2

Hi @mattiasthalen, here are two notes that might help:

  1. Note that the 2nd arguments to SVI is num_steps which in general is different from num_samples (and in practice often much larger). You may need to play around with both num_steps and the Adam(step_size=___) parameter to get things to converge. I often plot the time series of losses during convergence to ensure that the loss curve has indeed converged.
  2. Note that AutoNormal is a mean field guide and therefore assumes the posterior factorizes as independent posteriors over each latent variable. While I would expect AutoNormal to accurately discover the mode of your posterior and agree with MCMC (once you’ve tuned optimization), I would expect its posterior uncertainty to be tighter than the result of MCMC. To more accurately capture posterior uncertainty you can try other guide types, e.g. AutoLowRankmMultivariateNormal, custom guides, or learnable reparametrizers such as LocScaleReparam.
1 Like
3

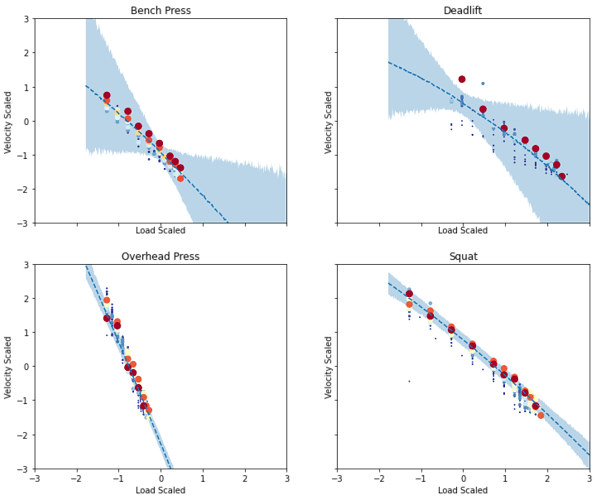
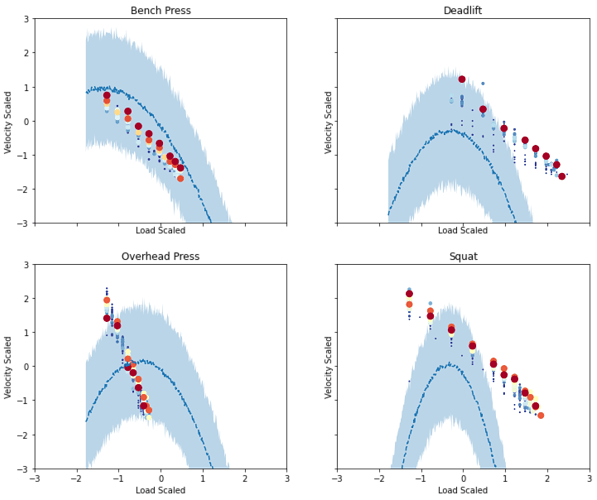
Thanks for the suggestion. Trying num_steps 1e6 made Colab cry :joy:. num_steps 1e5 works, but no luck in combo with step_size 1e-5.

Noob question, when plotting loss, how do you actually know it has converged?

4
  • If the loss is very noisy / choppy and seems to have no overall slope, then you probably want to decrease learning rate or maybe increase number of samples per svi step.
  • If the loss goes down and then plateaus, then the guide has probably converged :+1:
  • If the loss is not too choppy, but seems to be slowly and steadily decreasing, then you should probably run for longer.
2 Likes
5

@mattiasthalen you may also be interested in part 4 of our SVI tutorial, which contains general advice and best practices for troubleshooting and improving SVI results.

1 Like