Step-size and number of steps in NUTS

numpyro
1

Hi Numpyro users,

The forward problem:

We are trying out Bayesian inference for a problem with around 8 parameters. There are two kinds of model functions for us: (A) model_old which just returns the main diagonal — approximate eigenvalues — of a diagonally dominant matrix and compares it with observations, (B) model_new which calculates the exact eigenvalues — considering even the tiny off-diagonal elements.

What we expect vs. what we observe:

We are using NUTS sampler:

  • The model_old which does not need to do a eigenvalue calculation works great. It is slow in the warmup phase (due to increased number of steps per iterations) and much faster in the sampling stage (over time the number of steps per iterations decreases as the sampling progresses). It converges to the correct answers for our synthetic tests.
  • The model_new on the other hand behaves differently from what we expect. It has lower number of steps in the warmup phase and then when it goes into the sampling phase, the number of steps shoots up. We believe this should be the other way round? We think what might be happening is that after the warmup phase, it is reaching close to the minima of the loss function. At this point the gradient is very small and the step sizes are tiny resulting in many steps per iterations?

What we tried to remedy the problem but didn’t work:

From previous questions and discussions on this forum, we saw that a possible solution is to reduce the max_tree_depth in the sampling phase. So we changed it to 1 — meaning, it would take a max of 1 step in the sampling phase. The motivation behind doing this is that, we want NUTS to move close to the minima in the warmup phase and then once its sufficiently close, it just needs to sample that smaller area enough number of times, without investing much time in calculating the exact direction in which is should proceed. We are pretty confident that there is a single sharp minima and so once we ensure that it is in the vicinity of the minima, we just want a usual MCMC kind of stepping to map out the peak of the PDF. This is why we had set the max_tree_depth to 1. But surely, we are not understanding this correctly.

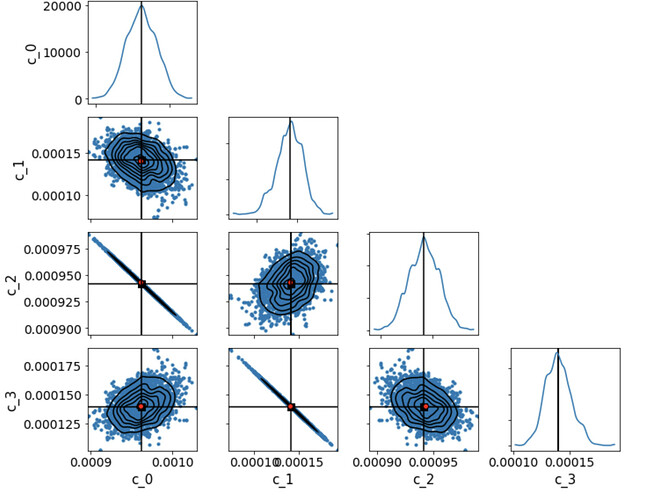
Below is what we get from model_old

Screen Shot 2021-11-26 at 12.33.06 AM
Screen Shot 2021-11-26 at 12.33.06 AM1474×1138 170 KB

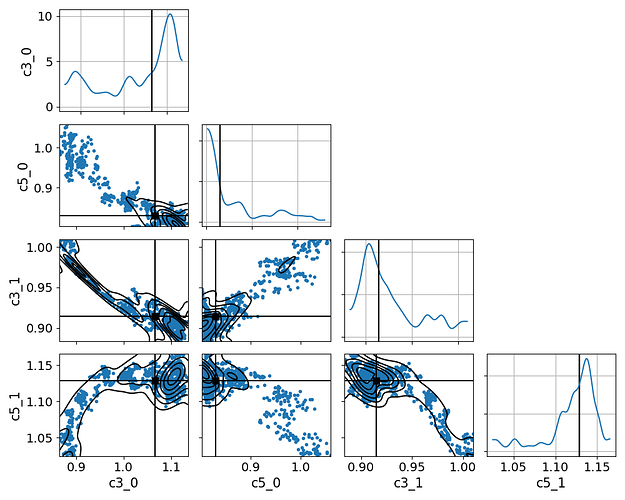
and what we get from model_new

corner-reduced-001
corner-reduced-0011000×800 103 KB

We even tried re-scaling the values of the parameters (as you will see in the axes labels) to make them of the order of unity.

The questions we want to ask:

  • In our understanding, since the two models return approximately the same predictions (by which I mean what is returned by the forward problem and is compared with the observations) how can the behaviour in the warmup and the sampling phase change so drastically? Does it matter so much that we are using an eigenvalue problem?
  • Is there a way to estimate the correct step-size apriori so that we can fix the step-size in the NUTS kernel initialization? We think that the problem with the results from model_new is because of the fact that the step-size it uses in the sampling phase is a constant and is larger than it needs to use.
  • Can we use the warmup of NUTS in the initial phase so that it approaches the minima of the posterior distribution and then shift to something less expensive like SA and take optimal steps so that it is essentially searching inside a grid close to the minima and simply mapping out the structure of the minima in the PDF? Again, we know we have a uni-modal solution which is quite sharply peaked.

P.S: After going over a lot of topics on the forum, I found that this is closest to the topic here posted by @campagne.

2

You can fix some step size and set adapt_step_size=False in the NUTS kernel. You might use an internal utility find_reasonable_step_size but it requires you to converge a numpyro model to a potential function (e.g. by using initialize_model)

Can we use the warmup of NUTS in the initial phase so that it approaches the minima of the posterior distribution and then shift to something less expensive like SA

I think you can use init_to_value strategy. We don’t expose inverse_mass_matrix in the SA kernel but please feel free to open a feature request (internally, we allow a custom inverse_mass_matrix but not expose it).

how can the behaviour in the warmup and the sampling phase change so drastically

It is hard to say. Typically, if NUTS behaves irregularity, then there might be some reasons:

  • precision is not good - consider to numpyro.enable_x64()
  • posterior is weird - consider various methods here
  • scale of parameters vary too much - consider to set regularize_mass_matrix=False in the kernel
  • step_size is not good (?) - maybe setting find_heuristic_step_size=True in the kernel will help, I’m not sure. Typically, its value can be controlled by setting target_accept_prob to 0.9 (to make step_size smaller) or 0.7 (to make step_size larger).
1 Like