Dear Experts
Below you will find 4 questions (Q1 to Q4) and hope that the code example is running for you for investigation. Of course your comments are welcome.
import scipy.integrate as integrate
import numpy as np
import jax
import jax.numpy as jnp
from jax import grad, jit, vmap
from jax import jacfwd, jacrev, hessian
from jax.ops import index, index_update
import numpyro
from numpyro.infer import NUTS, HMC, MCMC
class MixtureModel_jax():
def __init__(self, locs, scales, weights, *args, **kwargs):
super().__init__(*args, **kwargs)
self.loc = jnp.array([locs]).T
self.scale = jnp.array([scales]).T
self.weights = jnp.array([weights]).T
norm = jnp.sum(self.weights)
self.weights = self.weights/norm
self.num_distr = len(locs)
def pdf(self, x):
probs = jax.scipy.stats.norm.pdf(x,loc=self.loc, scale=self.scale)
return jnp.dot(self.weights.T,probs).squeeze()
def logpdf(self, x):
log_probs = jax.scipy.stats.norm.logpdf(x,loc=self.loc, scale=self.scale)
return jax.scipy.special.logsumexp(jnp.log(self.weights) + log_probs, axis=0)[0]
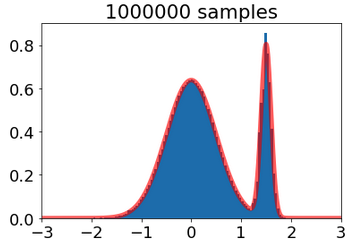
mixture_gaussian_model = MixtureModel_jax([0,1.5],[0.5,0.1],[8,2])
def phi(x):
return x**2
Integ_true,_=integrate.quad(lambda x: phi(x)*mixture_gaussian_model.pdf(x),-3,3)
rng_key = jax.random.PRNGKey(0)
_, rng_key = jax.random.split(rng_key)
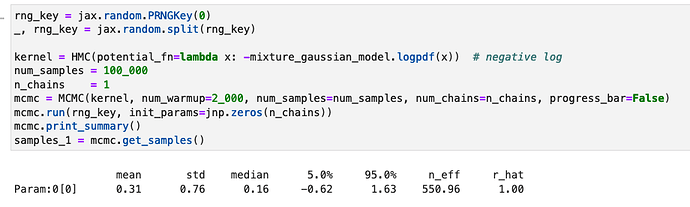
kernel = HMC(potential_fn=lambda x: -mixture_gaussian_model.logpdf(x)) # negative log
num_samples = 100_000
n_chains = 1
mcmc = MCMC(kernel, num_warmup=2_000, num_samples=num_samples, num_chains=n_chains)
mcmc.run(rng_key, init_params=jnp.zeros(n_chains))
samples_1 = mcmc.get_samples()
Then,
phi_spl1 = phi(samples_1)
Integ_HMC1 = np.mean(phi_spl1)
print(f"Integ_HMC:{Integ_HMC1:.6e}, err. relat: {np.abs(Integ_HMC1-Integ_true)/Integ_true:.6e}")
one gets
Integ_HMC:6.521168e-01, err. relat: 1.792710e-04
Now, If I run the same code with
num_samples = 100_000
n_chains = 10
I get,
Integ_HMC:6.608779e-01, err. relat: 1.361655e-02
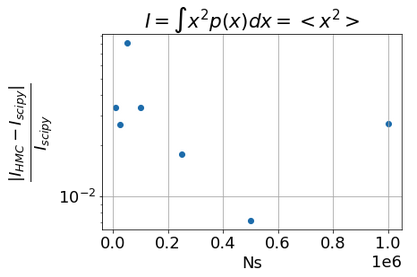
Q1: Why using 10 chains is worse then a single chain while I was expecting a 1/sqrt(10) better accuracy?
Now, using NUTS in place of HMC, with
num_samples = 100_000
n_chains = 1
I get
Integ_NUTS:6.545689e-01, err. relat: 3.940032e-03
and with
num_samples = 100_000
n_chains = 1
the result is
Integ_NUTS:6.580432e-01, err. relat: 9.268797e-03
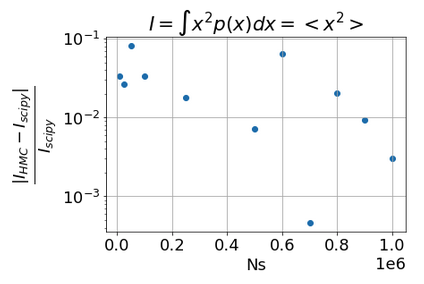
which shows also that running 10x more chains does not help at all.
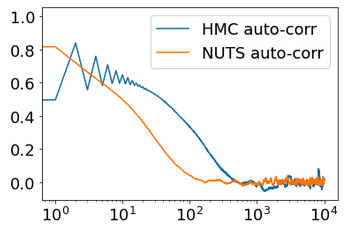
Q2: why NUTS not better than HMC?
Q3: As a side effect: the results were obtained on a CPU and I face the problem that running a single chain of 10^6 samples would get 30mins or so, while 10 chains of 10^5 samples each is done in 30sec?
Q4: running on a single GPU (K80) or even 4GPUs does not improve the running speed. Do you catch a reason for that?
Thanks for your advises.
PS: I have create an issue on Pyro github but I am not sure that it is the correct way. Hope that you can close the issue in case it was not the right way to ask the question.