I am using the following simple example to see how to use SVI for a Bayesian NN. Here is the code
from bokeh.plotting import figure, show
from bokeh.io import output_notebook
import numpy as np
import scipy.stats as stats
import jax.numpy as jnp
import jax.random as random
from jax.random import PRNGKey
import numpyro
import numpyro.distributions as dist
from numpyro.distributions import constraints
from numpyro.infer import Predictive, SVI, Trace_ELBO
output_notebook()
def actfun(x):
return jnp.tanh(x)
def model(x,N,data):
n_neurons = 2
w1 = numpyro.sample("w1",dist.Normal(jnp.zeros((1,n_neurons)),jnp.ones((1,n_neurons))) )
b1 = numpyro.sample("b1",dist.Normal(jnp.zeros((1,n_neurons)),jnp.ones((1,n_neurons))))
w2 = numpyro.sample("w2",dist.Normal(jnp.zeros((n_neurons,1)), jnp.ones((n_neurons,1))))
b2 = numpyro.sample("b2",dist.Normal(0., 1.))
out1 = actfun(jnp.matmul(x,w1)+b1)
y = jnp.matmul(out1,w2)+b2
sigma = numpyro.sample("sigma",dist.Beta(2.,2.))
numpyro.sample("obs",dist.Normal(y,sigma),obs=data)
def guide(x,N,data):
n_neurons = 2
w1_mean = numpyro.param("w1_mean",jnp.zeros((1,n_neurons)))
w1_var = numpyro.param("w1_var",jnp.ones((1,n_neurons)))
b1_mean = numpyro.param("b1_mean",jnp.zeros((1,n_neurons)))
b1_var = numpyro.param("b1_var",jnp.ones((1,n_neurons)))
w1 = numpyro.sample("w1",dist.Normal(w1_mean,w1_var) )
b1 = numpyro.sample("b1",dist.Normal(b1_mean,b1_var))
w2_mean = numpyro.param("w2_mean",jnp.zeros((n_neurons,1)))
w2_var = numpyro.param("w2_var",jnp.ones((n_neurons,1)))
b2_mean = numpyro.param("b2_mean",0.)
b2_var = numpyro.param("b2_var",1.)
w2 = numpyro.sample("w2",dist.Normal(w2_mean, w2_var))
b2 = numpyro.sample("b2",dist.Normal(b2_mean, b2_var))
out1 = actfun(jnp.matmul(x,w1)+b1)
y = jnp.matmul(out1,w2)+b2
sigma = numpyro.sample("sigma",dist.Beta(2.,2.))
# Generate data
N = 100
x = np.linspace(0,10,N)
data = 2*x + np.random.normal(0,0.5,N)
# Solve the SVI
optimizer = numpyro.optim.Adam(step_size=0.0005)
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
svi_result = svi.run(random.PRNGKey(0), 2000, jnp.atleast_2d(x).T, N, data)
# Sample the distribution of weights, biases and measurement standard deviation
predictive = Predictive(guide, params=svi_result.params, num_samples=1000)
samples = predictive(random.PRNGKey(1), jnp.atleast_2d(x).T,N, data)
# Use the model to predict the output
predictive_output = Predictive(model, samples)(PRNGKey(2), jnp.atleast_2d(x).T,N, None)["obs"]
# Plot the results
mean_prediction = jnp.mean(predictive_output, axis=0)
percentiles = np.percentile(predictive_output, [5.0, 95.0], axis=0)
p = figure()
p.cross(x,data)
p.line(x, mean_prediction)
show(p)
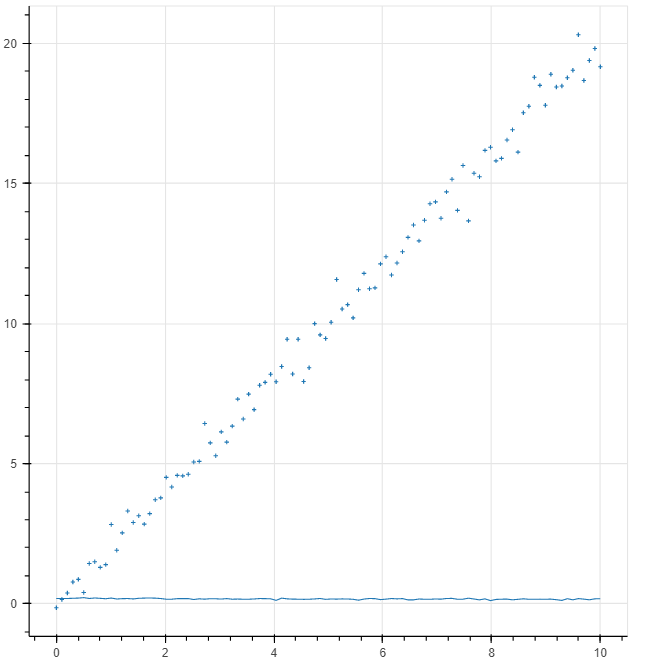
The code does not work. I get the following results. It seems that the NN it is not trained at all. Can you see where the mistake is?