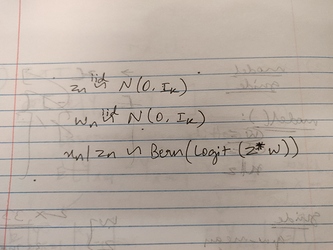Probabilistic PCA Tensor shape Broadcasting Error

[SiddheshA]

I’m working on Probabilistic PCA where the model assumes the following data generating process:

This model in Pyro:

def ppca_model(data):
    
    data_dim = data.shape[1]
    latent_dim = 2
    num_datapoints = data.shape[0]

    w_mean0 = torch.zeros([latent_dim, data_dim])
    w_std0 = torch.ones([latent_dim, data_dim])

    z_mean0 = torch.zeros([num_datapoints, latent_dim])
    z_std0 = torch.ones([num_datapoints, latent_dim])


    w = pyro.sample("w", pyro.distributions.Normal(loc = w_mean0, 
                                                   scale = w_std0))

    z = pyro.sample("z", pyro.distributions.Normal(loc = z_mean0, 
                                                   scale = z_std0))

    linear_exp = torch.exp(torch.matmul(z, w))    
    x = pyro.sample("x", pyro.distributions.Bernoulli(probs = linear_exp/(1+linear_exp)))

Given a one-hot-encoded data of dimension 3000 x 500, I try to infer latent variable z of dimension 3000 x 2.

Inference is attempted by HMC:

from pyro.infer.mcmc import HMC, MCMC

hmc_kernel = HMC(ppca_model, step_size=0.0855, num_steps=4)

mcmc_run = MCMC(hmc_kernel, num_samples=500, warmup_steps=100).run(x_new)

This breaks with the error message:

---

RuntimeError Traceback (most recent call last)
in
8 ppca_model(x_new)
9
—> 10 mcmc_run = MCMC(hmc_kernel, num_samples=500, warmup_steps=100).run(x_new)

~\Anaconda3\lib\site-packages\pyro\infer\abstract_infer.py in run(self, *args, **kwargs)
221 self._reset()
222 with poutine.block():
→ 223 for i, vals in enumerate(self._traces(*args, **kwargs)):
224 if len(vals) == 2:
225 chain_id = 0

~\Anaconda3\lib\site-packages\pyro\infer\mcmc\mcmc.py in _traces(self, *args, **kwargs)
266
267 def _traces(self, *args, **kwargs):
→ 268 for sample in self.sampler._traces(*args, **kwargs):
269 yield sample
270

~\Anaconda3\lib\site-packages\pyro\infer\mcmc\mcmc.py in _traces(self, *args, **kwargs)
204 progress_bar = ProgressBar(self.warmup_steps, self.num_samples, disable=self.disable_progbar)
205 self.logger = initialize_logger(self.logger, logger_id, progress_bar, log_queue)
→ 206 self.kernel.setup(self.warmup_steps, *args, **kwargs)
207 trace = self.kernel.initial_trace
208 with optional(progress_bar, not is_multiprocessing):

~\Anaconda3\lib\site-packages\pyro\infer\mcmc\hmc.py in setup(self, warmup_steps, *args, **kwargs)
380 self._args = args
381 self._kwargs = kwargs
→ 382 self._initialize_model_properties()
383
384 def cleanup(self):

~\Anaconda3\lib\site-packages\pyro\infer\mcmc\hmc.py in _initialize_model_properties(self)
353 self._trace_prob_evaluator = TraceEinsumEvaluator(trace,
354 self._has_enumerable_sites,
→ 355 self.max_plate_nesting)
356 if site_value is not None:
357 mass_matrix_size = sum(self._r_numels.values())

~\Anaconda3\lib\site-packages\pyro\infer\mcmc\util.py in init(self, model_trace, has_enumerable_sites, max_plate_nesting)
158 self._enum_dims = set()
159 self.ordering = {}
→ 160 self._populate_cache(model_trace)
161
162 def _populate_cache(self, model_trace):

~\Anaconda3\lib\site-packages\pyro\infer\mcmc\util.py in _populate_cache(self, model_trace)
170 raise ValueError("Finite value required for max_plate_nesting when model "
171 “has discrete (enumerable) sites.”)
→ 172 model_trace.compute_log_prob()
173 model_trace.pack_tensors()
174 for name, site in model_trace.nodes.items():

~\Anaconda3\lib\site-packages\pyro\poutine\trace_struct.py in compute_log_prob(self, site_filter)
214 if “log_prob” not in site:
215 try:
→ 216 log_p = site[“fn”].log_prob(site[“value”], *site[“args”], **site[“kwargs”])
217 except ValueError:
218 _, exc_value, traceback = sys.exc_info()

~\Anaconda3\lib\site-packages\torch\distributions\bernoulli.py in log_prob(self, value)
92 if self._validate_args:
93 self._validate_sample(value)
—> 94 logits, value = broadcast_all(self.logits, value)
95 return -binary_cross_entropy_with_logits(logits, value, reduction=‘none’)
96

~\Anaconda3\lib\site-packages\torch\distributions\utils.py in broadcast_all(*values)
35 break
36 values = [v if torch.is_tensor(v) else new_tensor(v) for v in values]
—> 37 return torch.broadcast_tensors(*values)
38
39

~\Anaconda3\lib\site-packages\torch\functional.py in broadcast_tensors(*tensors)
60 [0, 1, 2]])
61 “”"
—> 62 return torch._C._VariableFunctions.broadcast_tensors(tensors)
63
64

RuntimeError: The size of tensor a (500) must match the size of tensor b (2) at non-singleton dimension 1

At some point, it tries to broadcast tensors of dimension 3000 x 500 and 2. How do I solve this error? Or can somebody recommend any other inference technique that can work on this model?

[eb8680_2]

You need to observe your data:

linear = torch.matmul(z, w)  # no need to normalize these manually
x = pyro.sample("x", pyro.distributions.Bernoulli(logits = linear), 
                obs=data)

Also, if your data is actually one-hot encoded (i.e. only one entry per datapoint can be nonzero) you could use a OneHotCategorical as the likelihood:

x = pyro.sample("x", pyro.distributions.OneHotCategorical(logits = linear),
                obs=data)

[SiddheshA]

Thank you so much for the help, observing did help solve the HMC problem. I also changed to using the logits keyword instead of manually normalizing but kept Bernoulli since I have binary encoded columns and not one-hot encoded datapoints, so sorry for that confusion.

Also, in the mean time I tried inference with SVI and wrote this guide function for it:

def guide(data):
    data_dim = data.shape[1]
    latent_dim = 2
    num_datapoints = data.shape[0]
    
    qw_mean = pyro.param("qw_mean", torch.zeros([latent_dim, data_dim]))
    qw_stddv = pyro.param("qw_stddv", torch.ones([latent_dim, data_dim]),
                         constraint=constraints.positive)
    
    qz_mean = pyro.param("qz_mean", torch.zeros([num_datapoints, latent_dim]))
    qz_stddv = pyro.param("qz_stddv", torch.ones([num_datapoints, latent_dim]),
                         constraint=constraints.positive)
    
    w = pyro.sample("w", pyro.distributions.Normal(loc = qw_mean, 
                                                   scale = qw_stddv))
    z = pyro.sample("z", pyro.distributions.Normal(loc = qz_mean, 
                                                   scale = qz_stddv))
    
    linear_exp = torch.matmul(z, w)


    # observe data using the bernoulli likelihood
    
    x = pyro.sample("x", pyro.distributions.Bernoulli(logits = linear_exp))

Then called:

from pyro.infer import SVI, Trace_ELBO
import torch.distributions.constraints as constraints
from pyro.optim import Adam

adam_params = {"lr": 0.0005}
optimizer = Adam(adam_params)

svi = SVI(ppca_model, guide, optimizer, loss=Trace_ELBO())

n_steps = 2000

# do gradient steps
for step in range(n_steps):
    svi.step(x_train_tensors)
    if step % 100 == 0:
        print('.', end='')

That ended with a similar (broadcasting related) error in the pyro.infer.util add function:

~\Anaconda3\lib\site-packages\pyro\infer\util.py in add(self, *items)
112 assert all(f.dim < 0 and -value.dim() <= f.dim for f in frames)
113 if frames in self:
→ 114 self[frames] = self[frames] + value
115 else:
116 self[frames] = value

RuntimeError: The size of tensor a (13852) must match the size of tensor b (2) at non-singleton dimension 1

Any idea why that might be happening?

[eb8680_2]

You don’t need to sample x in your guide, since it’s observed. See part 2 of the language intro tutorial for more background.

[SiddheshA]

I’ve been following your recommendation but every time I change my model and guide I run into some error during inference. I tried making a neural network of the form

class NN(nn.Module):
    
    def __init__(self, input_size, hidden_size, output_size):
        super(NN, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.out = nn.Linear(hidden_size, output_size)
        
    def forward(self, x):
        output = self.fc1(x)
        output = F.relu(output)
        return output
def model(x_data, y_data):
    
    # Parameters for weights layer 1
    loc_w_1 = torch.zeros_like(net.fc1.weight)
    scale_w_1 = torch.ones_like(net.fc1.weight)
    # Parameters for biases layer 1
    loc_b_1 = torch.zeros_like(net.fc1.bias)
    scale_b_1 = torch.ones_like(net.fc1.bias)
    
    
    # Sample layer 1 weights and biases
    fc1w_prior = Normal(loc = loc_w_1, scale = scale_w_1)
    fc1b_prior = Normal(loc = loc_b_1, scale = scale_b_1)

    #######################################################################
    
    # Parameters for weights layer output
    loc_w_out = torch.zeros_like(net.out.weight)
    scale_w_out = torch.ones_like(net.out.weight)
    # Parameters for biases layer output
    loc_b_out = torch.zeros_like(net.out.bias)
    scale_b_out = torch.ones_like(net.out.bias)
    
    
    #  Sample layer output weights and biases
    outw_prior = Normal(loc = loc_w_out, scale = scale_w_out)
    outb_prior = Normal(loc = loc_b_out, scale = scale_b_out)
    
    ########################################################################
    
    priors = {'fc1.weight': fc1w_prior, 'fc1.bias': fc1b_prior,  'out.weight': outw_prior, 'out.bias': outb_prior}
    
    
    # lift module parameters to random variables sampled from the priors
    lifted_module = pyro.random_module("module", net, priors)
    # sample a regressor (which also samples w and b)
    lifted_reg_model = lifted_module()
    
    lhat = lifted_reg_model(x_data)
    scale = pyro.sample("sigma", Uniform(0., 10.))
    
    pyro.sample("obs", Delta(lhat), obs=y_data)

def guide(x_data, y_data):
    
    
    # Priors for weights layer 1
    fc1w_mu = torch.zeros_like(net.fc1.weight)
    fc1w_sigma = torch.ones_like(net.fc1.weight)
    
    # As param
    fc1w_mu_param = pyro.param("fc1w_mu", fc1w_mu)
    fc1w_sigma_param = pyro.param("fc1w_sigma", fc1w_sigma)
    
    # Sample
    fc1w_prior = Normal(loc=fc1w_mu_param, scale=fc1w_sigma_param)
    
    # Priois for biases layer 1
    fc1b_mu = torch.zeros_like(net.fc1.bias)
    fc1b_sigma = torch.ones_like(net.fc1.bias)
    
    # As param
    fc1b_mu_param = pyro.param("fc1b_mu", fc1b_mu)
    fc1b_sigma_param = pyro.param("fc1b_sigma", fc1b_sigma)
    
    # Sample
    fc1b_prior = Normal(loc=fc1b_mu_param, scale=fc1b_sigma_param)
    
    ###############################################################   
    # Priors for weights layer output
    outw_mu = torch.zeros_like(net.out.weight)
    outw_sigma = torch.ones_like(net.out.weight)
    
    # As param
    outw_mu_param = pyro.param("outw_mu", outw_mu)
    outw_sigma_param = pyro.param("outw_sigma", outw_sigma)
    
    # Sample
    outw_prior = Normal(loc=outw_mu_param, scale=outw_sigma_param).independent(1)
    
    
    # Priois for biases layer output
    outb_mu = torch.zeros_like(net.out.bias)
    outb_sigma = torch.ones_like(net.out.bias)
    
    # As param
    outb_mu_param = pyro.param("outb_mu", outb_mu)
    outb_sigma_param = pyro.param("outb_sigma", outb_sigma)
    
    # Sample
    outb_prior = Normal(loc=outb_mu_param, scale=outb_sigma_param)
    
    
    
    priors = {'fc1.weight': fc1w_prior, 'fc1.bias': fc1b_prior, 'out.weight': outw_prior, 'out.bias': outb_prior}
    
    lifted_module = pyro.random_module("module", net, priors)
    
    return lifted_module()

Running inference on this returns inf or nan loss at every batch and epoch. I’m guessing it could be because my data is all binary and sparse and I’ve changed the optimizers and learning rates to make the network learn but that doesnt seem to work too so I cant infer the weights of the network.

[eb8680_2]

In your latest example, you probably need to reduce the scales of your parameter initializations and approximate posterior distributions in your guide, just as you would with a non-Bayesian neural network. See e.g. the distributions used in torch.nn.init.