Hierarchical modeling

Tutorials
1

Hello, I am working through the Bayesian Hierarchical Linear Regression Numpyro tutorial. In short, the individual linear regression parameters (𝛼_i, 𝛽_i) come from the common group distributions parameterized by (𝜇_𝛼, 𝜎_𝛼, 𝜇_b, 𝜎_𝛽).

After the parameters are learned, the posterior mean of 𝛼 is much higher than that of 𝜇_𝛼.

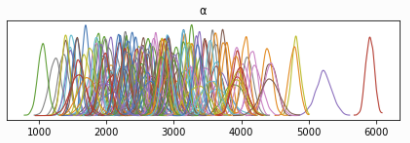
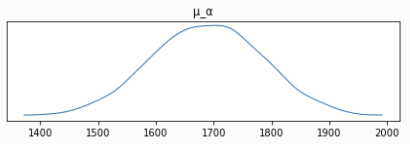
image

image

If 𝛼_i is from N ~ (𝜇_𝛼, 𝜎_𝛼), why is the posterior 𝜇_𝛼 (mean = 1691) not near the mean posterior 𝛼_i (mean = 2764)? Thanks!

2

I think it is because the prior for sigmas are quite flat. You might want to use a more informative priors for them. In addition, it is better to reparam those alpha_i sites, as in the Neal funnel example. The reason is: only alpha_i are used to generate observations and if the variance is large, values of mu will not play important role here - I guess you will get different results if you change the seed.

1 Like