Hello,
I am fairly new to Pyro and SVI in general, so forgive me if what I describe does not make sense. But I was looking to implement a model that can basically work on an N x M matrix where there are N observations of M variables.
For each of the N observations, there are some latent parameters/distributions.
For each of the M variables, I want to effectively perform a bayesian regression to predict each variable independently, but given the same set of latent observations.
To put it in other words, I have N samples and I want to perform M independent regressions on them. But in this case both N and M are very large (N can be in the millions and M can be in the thousands), so I am wondering what the best way to structure this type of model.
I was considering training a single model on each of the M variables totally independently, but then I would lose out on the shared latent properties between them. So is there any other option?
Could you write it out mathematically?
Yes, apologies for being unclear.
Put simply, I am trying to solve this system of equations for a matrix of N x M data:
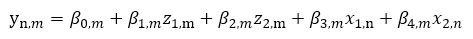
Where y corresponds to a value for a given observation/row (n) and independent variable/column (m). This value is predicted by an equation for which there are coefficients for each independent variable. Additionally, there are some unobserved latent variables (z) that globally effect each column. And some observed variables that we collect for each sample (x).
So I basically, I want to represent each column (m) as its own Linear layer, but I want to be able to consider variables that are shared across columns. And since I will potentially have thousands of columns, having thousands of linear layers that I would have to loop through in training sounds inefficient.
Please let me know if I can clarify further.
You could possibly do batch optimization over n and m if you assume that once \beta and z are given then the y_{nm} are independent (which they are). Then you could in principle use the ideas in this tutorial SVI Part II: Conditional Independence, Subsampling, and Amortization — Pyro Tutorials 1.8.4 documentation . Roughly the idea is that you can do stochastic updates so that you only consider a mini-batch of data at a time (a la neural networks). Let me know if this works/you need more details.
Hey, thanks for this. Looks very helpful for me. But I am a little confused about how your comments on batch optimization work practically.
Am I producing a plate for each of n and m, then training a Linear layer for each within the context of both of these?
So you would sample beta and z outside of the plate (which you could treat as your global random variables) and then inside a double plate you would sample the y[n][m] . I am assuming that you’d probably want to say something like
y = pyro.sample('y', dist.Normal(...))
inside of the plate. I guess you could use a delta so that it is exact but that seems like a bad idea.